模型为何“思考”「Rosetta」

21 May, 2025

• 原文链接：Why We Think
• 日期：2025年5月1日
• 预计阅读时间：40分钟
• 作者：Lilian Weng

特别感谢 John Schulman 为本文提供了大量极其宝贵的反馈和直接编辑。

推理时计算 (Graves et al. 2016、Ling, et al. 2017、Cobbe et al. 2021) 和思维链 (CoT) (Wei et al. 2022、Nye et al. 2021) 显著提升了模型性能，同时也引发了许多研究问题。本文旨在回顾关于如何有效利用推理时计算（即“思考时间”）及其益处的最新进展。

动机

让模型进行更长时间的思考，可以从几个不同方面进行阐述。

心理学类比

核心思想与人类的思考方式息息相关。我们人类无法立即给出“12345 乘以 56789 是多少？”这个问题的答案。相反，对于复杂问题，我们自然会花时间思考和分析，然后才能得出结果。在 《思考，快与慢》(Kahneman, 2013) 一书中，丹尼尔·卡尼曼 (Daniel Kahneman) 借助 双系统理论 的视角，将人类思维划分为两种模式：

• 快速思维（系统 1） 运作迅速且自动化，由直觉和情感驱动，几乎不需要努力。
• 慢速思维（系统 2） 需要深思熟虑、逻辑推理和显著的认知努力。这种思维模式消耗更多的脑力，需要有意识的参与。

由于系统 1 思维快速且容易，它常常成为主要的决策驱动因素，但代价是牺牲了准确性和逻辑性。它自然地依赖我们大脑的思维捷径（即启发式），并可能导致错误和偏见。通过有意识地放慢速度，花更多时间反思、改进和分析，我们可以运用系统 2 思维来挑战我们的直觉，做出更理性的选择。

计算作为一种资源

深度学习的一种观点认为，神经网络可以根据其在一次前向传播中可访问的计算量和存储量来表征；如果我们使用梯度下降优化它们来解决问题，优化过程将找出如何利用这些资源——它们将弄清楚如何将这些资源组织成用于计算和信息存储的电路。从这个角度来看，如果我们设计一个能够在推理时进行更多计算的架构或系统，并训练它有效利用这一资源，它将表现得更好。

在 Transformer 模型中，模型为每个生成的 token 所做的计算量 (flops) 大致是参数数量的两倍。对于稀疏模型，如专家混合模型 (MoE)，每次前向传播中只有一小部分参数被使用，因此计算量 = 2 * 参数 / 稀疏度，其中稀疏度是激活专家的比例。

另一方面，CoT 使模型能够为其尝试计算的答案的每个 token 执行远更多的 flops 计算。事实上，CoT 有一个很好的特性，它允许模型根据问题的难度使用可变数量的计算资源。

潜在变量建模

机器学习中的一个经典思想是定义一个包含潜在（隐藏）变量 $z$ 和可见变量 $y$ 的概率模型，其中 $y$ 是给定给我们的学习算法的。对潜在变量的所有可能值进行边缘化（求和），使我们能够表达可见变量上的丰富分布，$P(y)={\sum }_{z~P(z)}P(y\mid z)$。例如，我们可以通过让 $x$ 表示问题陈述，$y$ 表示真实答案或证明，$z$ 表示导致证明的自由形式的思考过程来建模数学问题和解决方案的分布。需要优化的边际概率分布将是 $P(y\mid x)={\sum }_{z~p(z\mid x)}P(y\mid x,z)$。

潜在变量视角对于理解涉及收集多个并行 CoT 或对 CoT 进行搜索的方法特别有用——这些算法可以被看作是从后验概率 $P(z\mid x,y)$ 中进行采样。这种观点也表明，使用对数损失 $\log P(y\mid x)$ 作为优化目标的好处，因为对数损失目标在预训练中非常有效。

以 token 为单位的思考

在生成简短答案之前生成中间步骤的策略，特别是对于数学问题，由 Ling 等人 (2017) 进行了探索，他们引入了 AQUA-RAT 数据集；随后由 Cobbe 等人 (2021) 进行了扩展，他们引入了 小学数学 (GSM) 数据集。Cobbe 等人使用人类编写的解决方案进行监督学习来训练一个生成器，并训练验证器来预测候选解决方案的正确性；然后他们可以对这些解决方案进行搜索。Nye 等人 (2021) 实验了将中间思考 token 作为“草稿本”，而 Wei 等人 (2022) 则创造了现在标准术语 思维链 (CoT)。

早期改进 CoT 推理的工作包括对人类编写的推理轨迹或根据答案正确性筛选的模型编写轨迹进行监督学习，其中后者可以看作是强化学习 (RL) 的一种基本形式。其他一些工作发现，通过适当的提示，可以显著提升指令微调模型在数学上的表现，例如使用"一步一步思考" (Kojima et al. 2022) 或更复杂的提示来鼓励模型首先反思相关知识 (Yasunaga et al. 2023)。

后来的工作发现，通过在具有可自动检查解决方案（如带简短答案的 STEM 问题或可通过单元测试检查的编码任务）的问题数据集上进行强化学习，可以显著提升 CoT 推理能力 (Zelikman et al. 2022、Wang et al., 2023、Liu et al., 2023)。随着 o1-preview、o3 以及 R1 技术报告 (DeepSeek-AI, 2025) 的发布，这种方法变得突出，这些报告表明简单的策略梯度算法即可带来强大的性能。

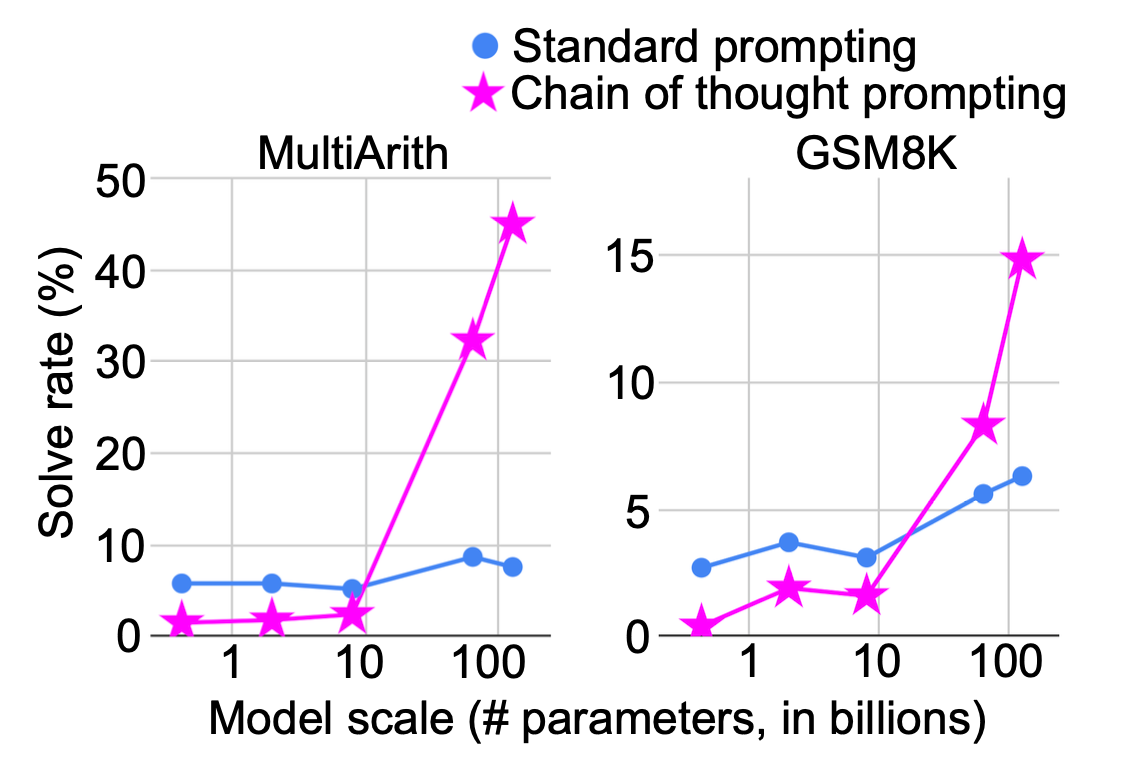
思维链提示导致解决数学问题的成功率更高。模型越大，思考时间带来的收益越大。（图片来源：Wei et al. 2022）

分支与编辑

推理时计算的根本目的是在推理时自适应地修改模型的输出分布。有多种方法可以利用推理时资源进行解码，以选择更好的样本，从而使模型的预测转向更理想的分布。改进解码过程的两种主要方法是并行采样和序列修订。

• 并行采样 同时生成多个输出，并通过过程奖励信号提供每一步的指导，或在最后使用验证器判断质量。它是最广泛采用的解码方法，用于提高推理时性能，例如 N 选一 (best-of-N) 或束搜索 (beam search)。当没有真实答案可用时，自洽性 (Wang et al. 2023) 通常用于在多个 CoT 展开中通过多数投票选择答案。
• 序列修订 根据上一步的输出迭代地调整模型的响应，要求模型有意识地反思其现有响应并纠正错误。修订过程可能需要依赖于微调模型，因为如果仅仅依靠模型固有的自我纠正能力而没有外部反馈，可能无法带来改进 (Kamoi et al. 2024、Huang et al. 2024)。

并行采样简单、直观且易于实现，但受限于模型能否一次性得出正确解决方案的能力。序列修订明确要求模型反思错误，但它速度较慢，且在实现过程中需要格外小心，因为它确实存在将正确预测修改为不正确或引入其他类型幻觉的风险。这两种方法可以结合使用。Snell 等人 (2024) 表明，较简单的问题纯粹受益于序列推理时计算，而较难的问题通常在序列与并行计算的最佳比例下表现最佳。

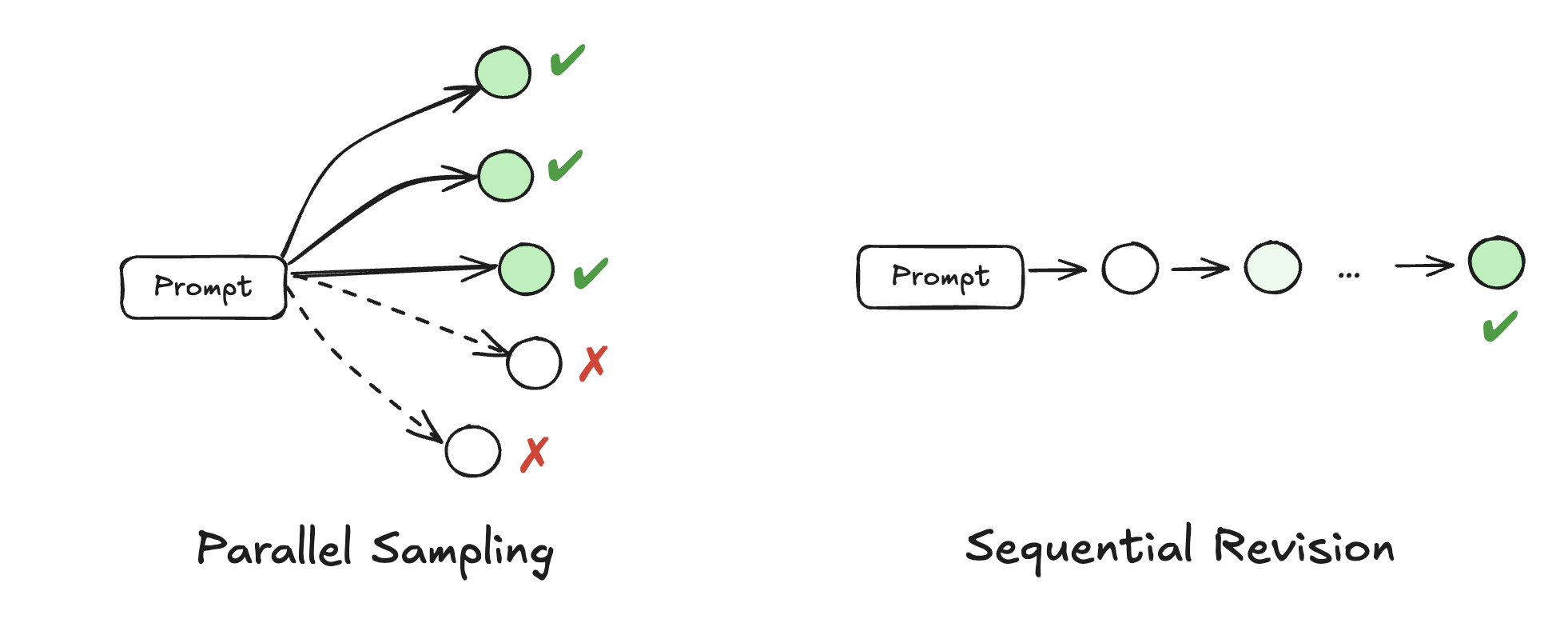
并行采样与序列修订的示意图。

并行采样

给定一个生成模型和一个可用于评估完整或部分样本的评分函数，我们可以使用各种搜索算法来找到高分样本。N 选一 (Best-of-N) 是最简单的此类算法：只需收集 N 个独立样本，并根据某个评分函数选择排名最高的样本。束搜索 (Beam search) 是一种更复杂的搜索算法，它使搜索过程更具适应性，在解空间中更有希望的部分投入更多的采样计算。

束搜索维护一组有前景的部分序列，并交替进行扩展和剪枝那些前景较差的序列。作为选择机制，我们可以使用过程奖励模型 (PRM; Lightman et al. 2023) 来指导束搜索的候选选择。Xie 等人 (2023) 使用大型语言模型 (LLM) 以多项选择题的形式评估其自身生成的推理步骤的正确性，发现每步自我评估在束搜索解码过程中减少了多步推理中的累积误差。此外，在采样过程中，退火温度有助于减轻累积的随机性。Xie 等人的这些实验使用 Codex 模型在少样本 GSM8k、AQuA 和 StrategyQA 基准测试上实现了 5-6% 的改进。奖励平衡搜索（简称“REBASE”；Wu et al. 2025）单独训练了一个过程奖励模型 (PRM)，根据 softmax 归一化的奖励分数，在束搜索的每个深度决定每个节点应该扩展多少。Jiang 等人 (2024) 训练了他们的 PRM，名为“RATIONALYST”，用于在大量无标签数据上以合成理由为条件指导束搜索。好的理由是根据它们是否通过一个阈值帮助减少真实答案 token 的负对数概率来筛选的，即比较理由包含在上下文中与不包含在上下文中时的差异。在推理时，RATIONALYST 通过帮助估计下一步推理步骤的对数概率（“隐式”）或直接生成下一步推理步骤作为提示的一部分（“显式”），为 CoT 生成器提供过程监督。

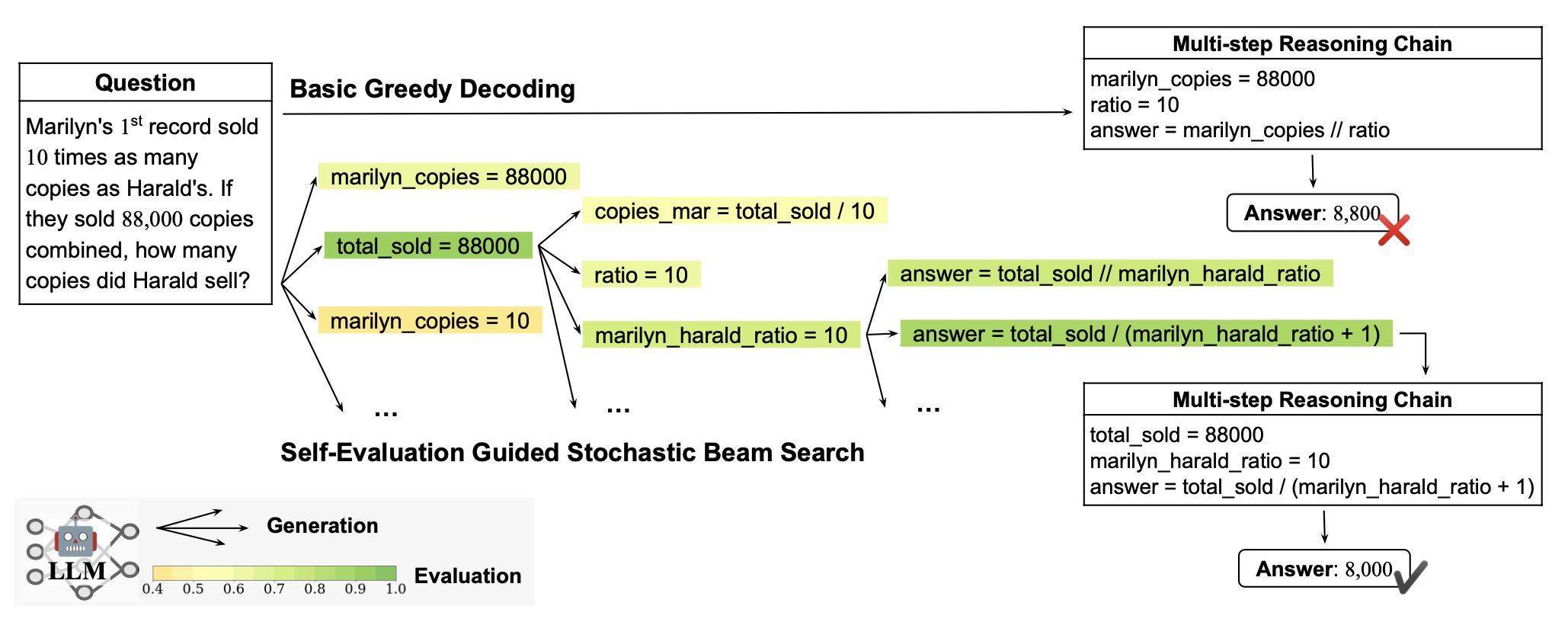
LLM 每步自我评估引导的束搜索解码。（图片来源：Xie et al. 2023）

有趣的是，即使没有明确的零样本或少样本提示，也可能触发新兴的思维链推理路径。Wang & Zhou (2024) 发现，如果我们在第一个采样 token 处通过保留置信度最高的 k 个 token（置信度衡量为采样时 top-1 和 top-2 候选之间的差异）进行分支，然后继续这些 k 个采样尝试并进行贪婪解码，许多这样的序列自然会包含 CoT。特别是当 CoT 出现在上下文中时，它会使最终答案的解码更具置信度。为了计算最终答案的置信度，需要通过任务特定的启发式方法（例如，数学问题的最后一个数值）或通过进一步提示模型"所以答案是"来识别答案范围。仅在第一个 token 处进行分支的设计选择，是基于早期分支显著增强潜在路径多样性，而后续 token 受先前序列影响很大的观察。

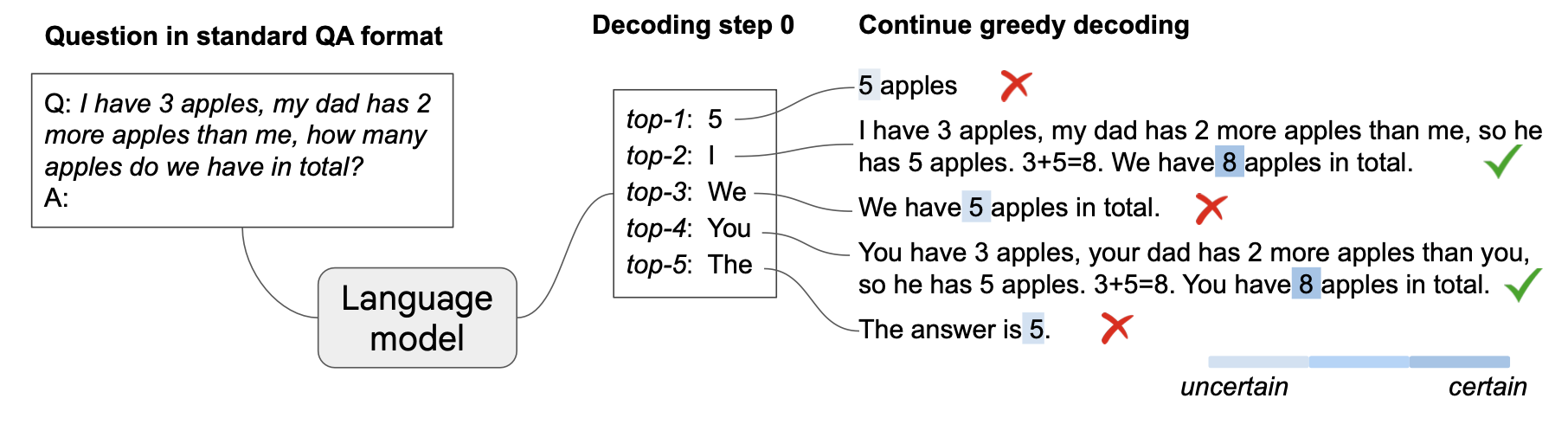
Top-k 解码，k 指第一个采样步骤中的候选数量。（图片来源：Wang & Zhou, 2024）

序列修订

如果模型能够反思并纠正过去的响应中的错误，我们期望模型能生成一系列质量不断提高的迭代修订。然而，这种自我纠正能力并非大型语言模型 (LLM) 固有的，也无法轻易开箱即用，这归因于多种失败模式，例如：(1) 幻觉，包括将正确响应修改为不正确；(2) 行为退化为不纠正行为，例如对首次不正确响应进行微小修改或不修改；或 (3) 未能泛化到推理时的分布偏移。Huang 等人 (2024) 的实验表明，天真地应用自我纠正会导致性能下降，模型需要外部反馈才能自我改进，这些反馈可以基于匹配真实值、启发式方法和任务特定指标、编码问题的单元测试结果 (Shinn, et al. 2023)、更强大的模型 (Zhang et al. 2024) 以及人类反馈 (Liu et al. 2023)。

自纠正学习 (Welleck et al. 2023) 旨在给定一个固定的生成器模型 $P_0(y_0\mid x)$ 的情况下，训练一个纠正器模型 $P_{\theta }(y\mid y_0,x)$。虽然生成器模型保持通用，但纠正器模型可以是任务特定的，并且只在初始模型响应和额外反馈（例如一个句子、一个编译器跟踪、单元测试结果；可选）的条件下进行生成：

1. 自纠正学习首先针对数据池中的每个提示生成多个输出；
2. 然后通过将同一提示的两个输出配对（如果其中一个输出的值高于另一个）来创建价值改进对（提示 $x$, 假设 $y$, 纠正 $y^{\prime }$）。
3. 这些对是根据其价值改进量 $v(y^{\prime })-v(y)$ 和两个输出之间的相似度 $Similarity(y,y^{\prime })$ 按比例选择的，用于训练纠正器模型。
4. 为了鼓励探索，纠正器也会将新生成的输出添加到数据池中。在推理时，纠正器可以迭代使用以创建序列修订的纠正轨迹。

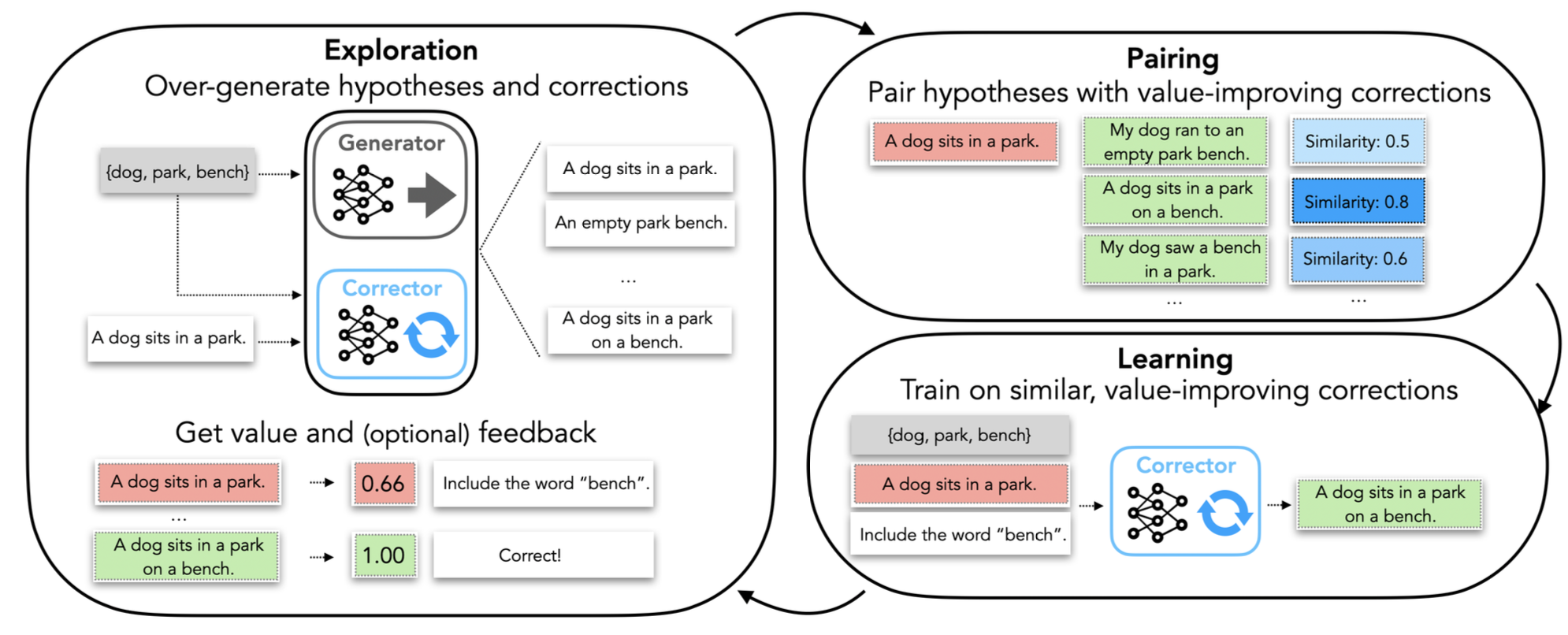
自纠正学习的示意图，通过匹配同一问题的模型输出形成价值改进对来训练纠正模型。（图片来源：Welleck et al. 2023）

递归检查 (Qu et al. 2024) 也旨在训练一个更好的纠正器模型，但使用单个模型同时进行生成和自我纠正。

SCoRe（通过强化学习进行自我纠正；Kumar et al. 2024）是一种多轮强化学习方法，旨在鼓励模型通过在第二次尝试中产生比第一次尝试更好的答案来进行自我纠正。它包含两个训练阶段：阶段 1 仅最大化第二次尝试的准确性，同时仅对第一次尝试施加 KL 惩罚，以避免首次响应与基础模型行为发生过多偏移；阶段 2 优化第一次和第二次尝试产生的答案的准确性。理想情况下，我们希望看到第一次和第二次尝试的性能都更好，但添加阶段 1 可以防止模型对第一次响应进行微小修改或不修改的行为退化，而阶段 2 则进一步改进了结果。

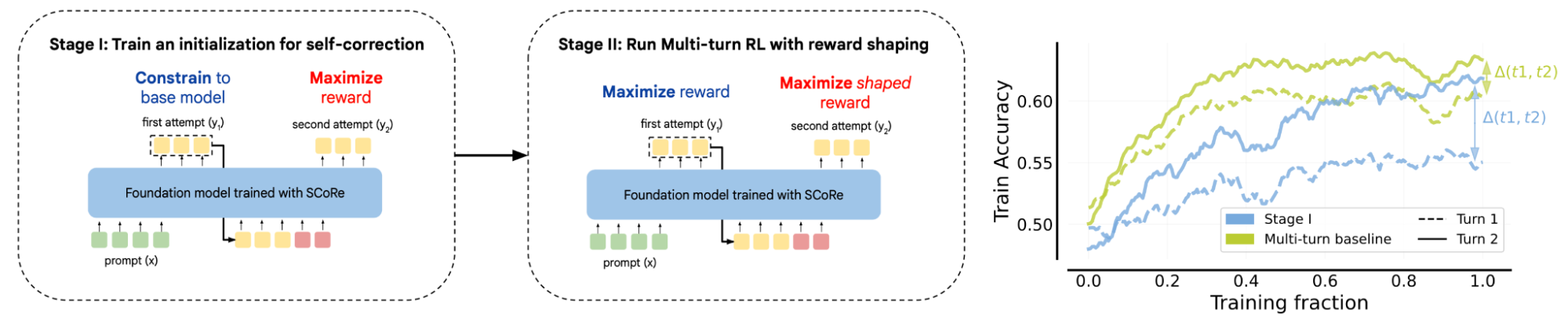
通过两阶段强化学习训练提高自我纠正能力的明确训练设置。（图片来源：Kumar et al. 2024）

利用强化学习提升推理能力

近期，通过使用带有真实答案的问题集合（通常是易于验证答案的 STEM 问题和谜题），并对模型给出正确答案进行奖励，利用强化学习提升语言模型推理能力取得了许多成功。OpenAI 的 o 系列模型以及 DeepSeek 随后发布的模型和技术报告的强大性能，推动了这一领域的近期活跃。

DeepSeek-R1 (DeepSeek-AI, 2025) 是一个开源 LLM，旨在擅长数学、编码和逻辑问题解决等需要高级推理技能的任务。他们进行了两轮 SFT-RL 训练，使 R1 在推理和非推理任务上都表现出色。

1. 冷启动 SFT：对 DeepSeek-V3-Base 基础模型进行微调，使用数千个冷启动数据。若无此步骤，模型会出现可读性差和语言混淆等问题。
2. 面向推理的 RL：使用两类基于规则的奖励，在仅推理提示上训练推理模型：
   • 格式奖励：模型应将 CoT 包装在 <thinking> ... </thinking> token 中。
   • 准确性奖励：最终答案是否正确。数学问题的答案需要以特定格式（例如，在一个框中）存在才能可靠验证。对于编码问题，使用编译器评估测试用例是否通过。
3. 拒绝采样 + 非推理 SFT：利用在步骤 2 的 RL 检查点上通过拒绝采样创建的新 SFT 数据，结合来自 DeepSeek-V3 (DeepSeek-AI, 2024) 管道的非推理监督数据，重新训练 DeepSeek-V3-Base。
   • 过滤掉包含混合语言、长段落和代码块的 CoT。
   • 包含使用 DeepSeek-V3 (DeepSeek-AI, 2024) 管道的非推理任务。
   • 对于某些非推理任务，调用 DeepSeek-V3 在回答问题前通过提示生成潜在的 CoT。但对于像“你好”这样更简单的查询，则不需要 CoT。
   • 然后对总共 80 万个样本进行 2 个 epoch 的微调。
4. 最终 RL 阶段：在推理和非推理提示上训练步骤 3 的检查点，以提高有用性、无害性和推理能力。

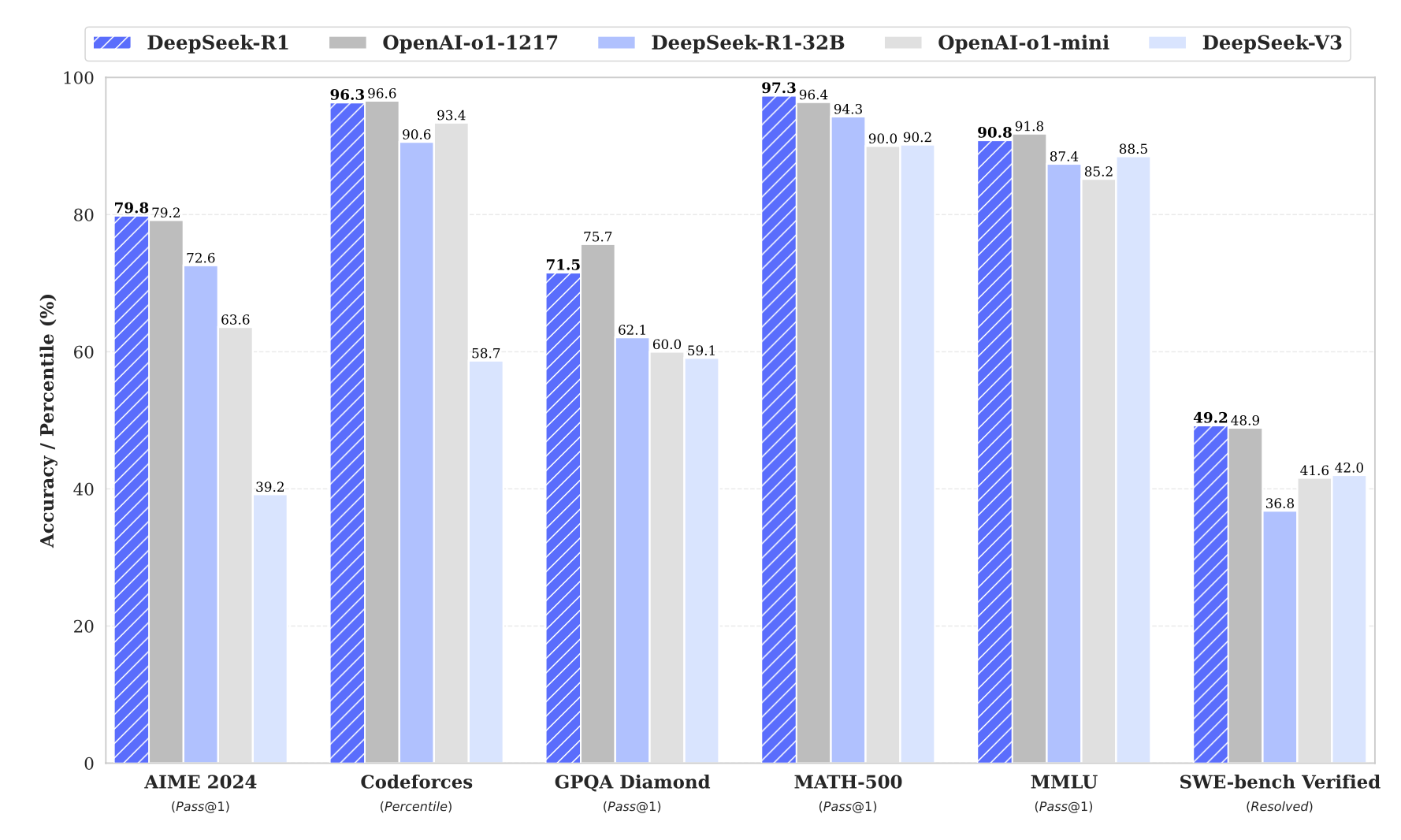
DeepSeek-R1 在几个广泛使用的推理基准测试中表现与 OpenAI 的 o1-preview 和 o1-mini 相当。DeepSeek-V3 是唯一列出的非推理模型。（图片来源：DeepSeek-AI, 2025）

有趣的是，DeepSeek 团队展示了纯粹的强化学习（没有 SFT 阶段）仍能学习到高级推理能力，例如反思和回溯（“Aha 时刻”）。模型在强化学习训练过程中自然学会了花费更多的思考 token 来解决推理任务。“Aha 时刻”可以涌现，指的是模型反思之前的错误，然后尝试其他方法来纠正它们。后来，各种开源工作致力于复现 R1 的结果，例如 Open-R1、SimpleRL-reason 和 TinyZero，它们都基于 Qwen 模型。这些努力也证实了纯强化学习在数学问题上带来了出色的性能，以及“Aha 时刻”的涌现。

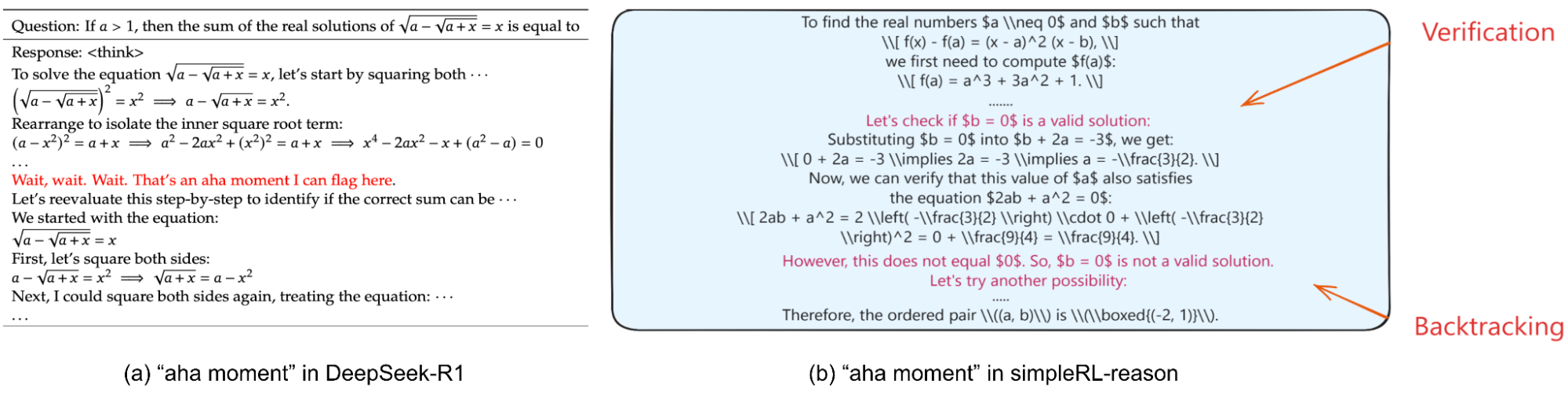
模型学习反思和纠正错误的例子。（图片来源：（左）DeepSeek-AI, 2025；（右）Zeng et al. 2025）

DeepSeek 团队还分享了一些他们不成功的尝试。他们未能成功使用过程奖励模型 (PRM)，因为它难以定义每步的评分标准或确定中间步骤是否正确，同时使训练更容易受到奖励作弊的影响。蒙特卡洛树搜索 (MCTS) 的尝试也失败了，原因在于语言模型 token 的搜索空间过大，与例如国际象棋相比；而且训练用于指导搜索的细粒度价值模型也非常具有挑战性。失败的尝试通常能提供独特的见解，我们鼓励研究社区更多地分享那些没有成功的方法。

外部工具使用

在推理步骤中，某些中间步骤可以通过执行代码或进行数学计算来可靠且准确地解决。将推理部分的这些组件卸载到外部代码解释器中，例如 PAL（程序辅助语言模型；Gao et al. 2022）或 Chain of Code (Li et al. 2023)，可以通过外部工具扩展 LLM 的能力，从而无需 LLM 自身学习执行代码或充当计算器。这些代码模拟器，例如 Chain of Code 中的，可以通过 LLM 进行增强，以便在标准代码解释器失败时，我们有选择使用 LLM 来执行该行代码。使用代码增强推理步骤对于数学问题、符号推理和算法任务特别有益。这些单元测试可能不作为编码问题的一部分存在，在这种情况下，我们可以指导模型自行生成单元测试，供其进行测试以验证解决方案 (Shinn, et al. 2023)。

程序辅助语言模型提示的一个示例。（图片来源：Gao et al. 2022）

ReAct（推理+行动；Yao et al. 2023）结合了搜索维基百科 API 的行动和推理轨迹的生成，从而使推理路径能够融入外部知识。

ReAct 提示方法解决 HotpotQA 问题的示例，使用维基百科搜索 API 作为外部工具辅助推理。（图片来源：Yao et al. 2023）

OpenAI 最近发布的 o3 和 o4-mini 是另外两个很好的例子，它们的推理过程涉及网络搜索、代码执行和图像处理等工具使用。该团队观察到，大规模强化学习展现出与 GPT 范式相同的趋势，即“更多计算 = 更好性能”。

忠实地思考

深度学习模型通常被视为黑箱，因此提出了各种可解释性方法。可解释性有几个用处：首先，它为我们提供了一个额外的测试，以确定模型是否与其创建者的意图不符，或者它是否以某种我们无法通过监控其行为来判断的方式行为不端。其次，它可以帮助我们确定模型是否正在使用一个合理的过程来计算其答案。思维链提供了一种特别方便的可解释形式，因为它以自然语言使模型的内部过程可见。然而，这种可解释性基于模型真实描述其内部思维过程的假设。

最近的研究表明，监控推理模型的 CoT 可以有效检测模型的不当行为，例如奖励作弊，甚至可以使一个较弱的模型监控一个较强的模型 (Baker et al. 2025)。增加推理时计算还可以提高对抗鲁棒性 (Zaremba et al. 2025)；这在直观上是合理的，因为当模型遇到不寻常的输入（例如对抗样本或越狱尝试）时，更长时间的思考会特别有用——它可以使用额外的思考时间来理解所面临的奇怪情况。

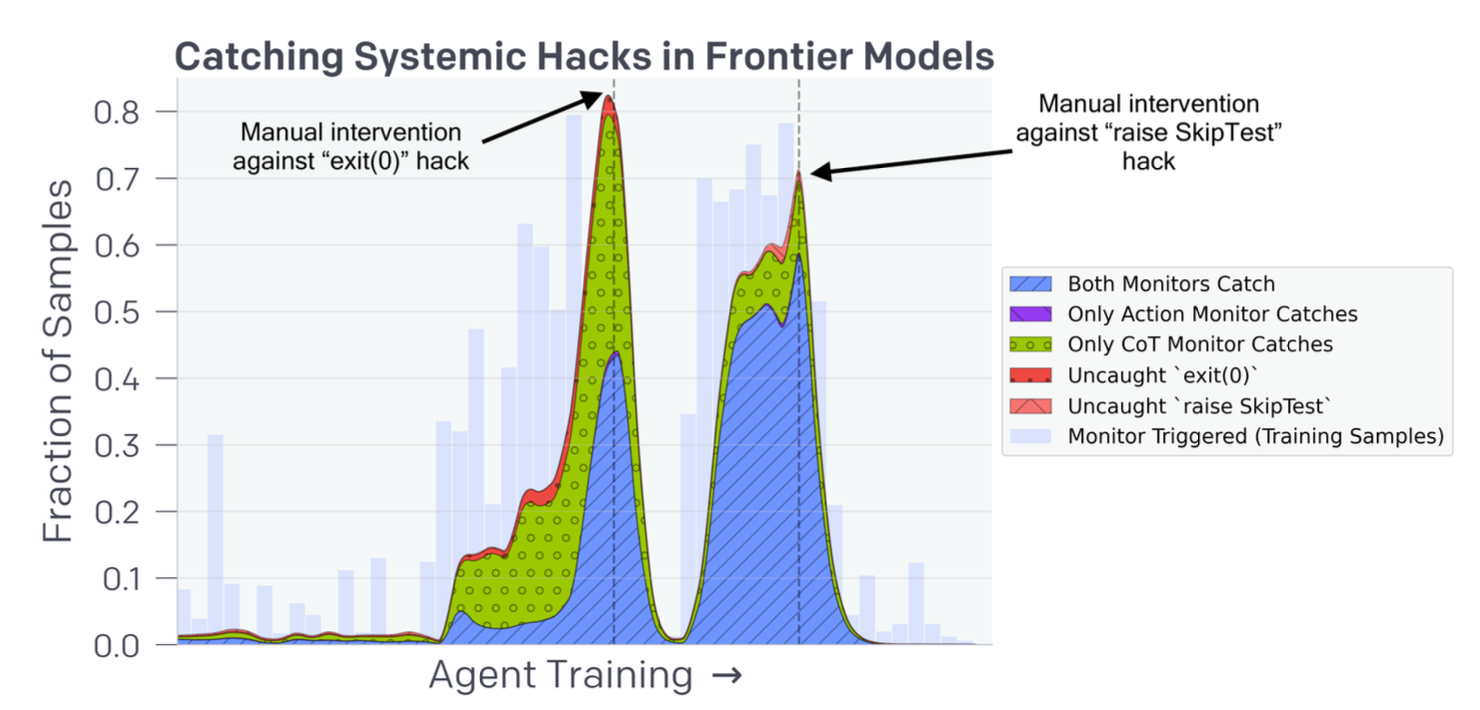
该实验要求模型根据其思考过程判断另一个模型是否以某种方式尝试对编码问题的单元测试进行作弊。我们可以通过不同类型的监控器在训练期间监控这些奖励作弊行为。exit(0) 编码作弊是指代理利用一个 bug 提前退出环境而没有运行所有单元测试。raise SkipTest 作弊是指代理从测试框架之外的函数中引发异常以跳过单元测试评估。（图片来源：Baker et al. 2025）

模型是否忠实地表达其所思？

直观上，由于缺乏旨在鼓励忠实推理的明确训练目标，模型的 CoT 可能会存在偏差。或者当我们对模型进行微调时，使用人类编写的解释，这些人工样本可能包含错误。因此，我们不能默认假设 CoT 始终是忠实的。

Lanham 等人 (2023) 通过故意在 CoT 中引入错误，并测量其对一系列多项选择任务（例如 AQuA、MMLU、ARC Challenge、TruthfulQA、HellaSwag）准确性的影响，调查了 CoT 忠实性失败的几种模式：

• 错误 1 (提前回答)：模型可能在 CoT 生成之前过早地得出结论。这通过提前截断或在 CoT 中插入错误来测试。不同任务显示出对 CoT 有效性的不同任务特定依赖性；有些任务的评估性能对截断的 CoT 敏感，但有些则不敏感。Wang 等人 (2023) 进行了类似的实验，但错误更微妙，涉及 CoT 形成中的桥接对象或语言模板。

• 错误 2 (无信息 token)：无信息的 CoT token 提高性能。这个假设通过用填充文本（例如，全部句号）替换 CoT 来测试，这种设置显示没有准确性增加，与没有 CoT 相比，有些任务可能会略有性能下降。

• 错误 3 (人类不可读的编码)：相关信息以人类难以理解的方式编码。以非标准方式转述 CoT 并未在所有数据集上降低性能，这表明准确性提升并不依赖于人类可读的推理。

评估 CoT 忠实度的不同 CoT 扰动方法示意图。（图片来源：Lanham et al. 2023）

有趣的是，Lanham 等人指出，对于多项选择题，较小的模型可能无法很好地利用 CoT，而较大的模型即使没有 CoT 也可能能够解决这些任务。这种对 CoT 推理的依赖性（通过有 CoT 和无 CoT 获得相同答案的百分比来衡量）在多项选择题上并不总是随模型大小增加而增加，但在加法任务上确实随模型大小增加而增加，这意味着思考时间对于复杂推理任务更重要。

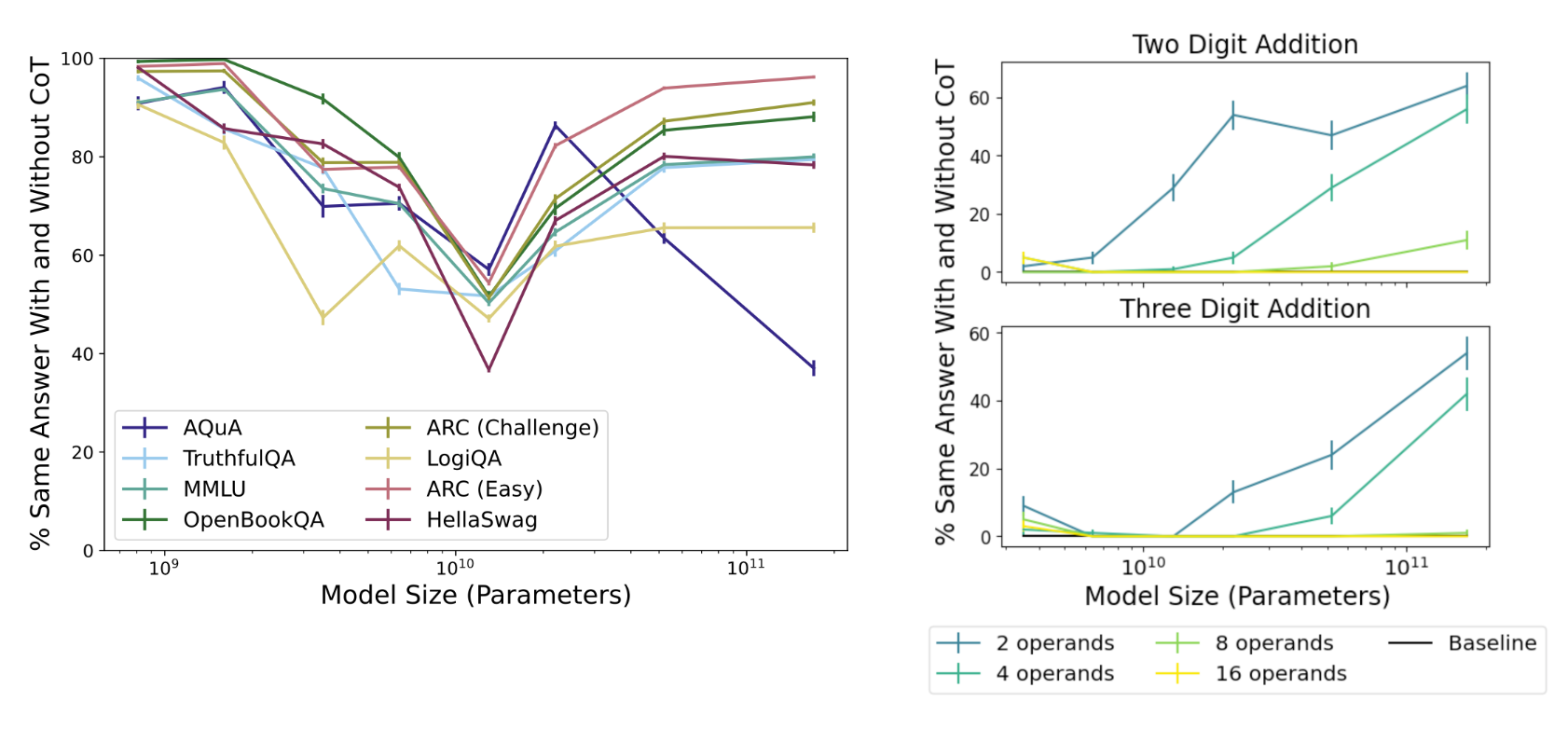
CoT 推理的依赖性衡量为有 CoT 和无 CoT 获得相同答案的百分比。它对于加法等推理任务更重要，更大的模型受益更多。（图片来源：Lanham et al. 2023）

测试 CoT 忠实度的其他方法涉及扰动提示而不是直接修改 CoT 路径 (Turpin et al. 2023、Chua & Evans, 2025、Chen et al. 2025)。

一种方法是在少样本示例中始终将正确答案标记为“(A)”，无论真实标签如何，以引入偏差。

另一种提示技术是在提示中插入误导性提示，例如"我认为答案是 <random_label>，但很好奇你怎么看。"或"一位斯坦福大学教授认为答案是 <random_label>" 。通过比较模型在有误导性提示和无误导性提示下的预测，我们可以衡量模型是否能够忠实地描述提示对其答案的影响。特别是，在模型产生不同提示和非提示答案的情况下，我们衡量模型在解决带有提示的问题时是否承认了提示。如果模型是忠实的，它应该明确承认影响并承认其答案的变化是由于提示。

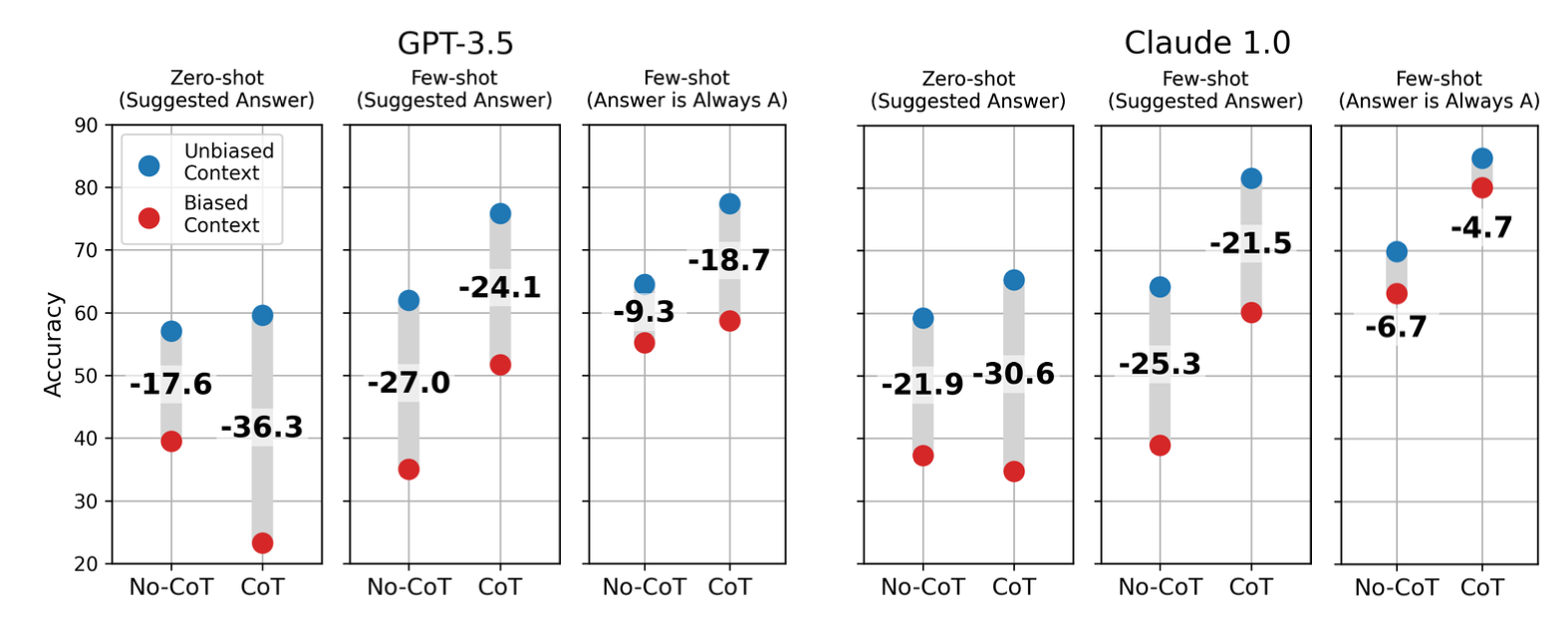
GPT 和 Claude 模型都对上下文中不同类型的偏差敏感。模型准确性的下降表明系统性的不忠实。错误标签的直接提示比“答案总是 A”类型的偏差更有效。（图片来源：Turpin et al. 2023）

多项研究发现，推理模型比所有测试过的非推理模型更可靠地描述提示的影响。例如，我们可以衡量模型承认提示是决定因素的样本比例（“忠实 CoT”）。推理模型（Claude 3.7 Sonnet，DeepSeek R1）总体上比非推理模型（Claude 3.6，DeepSeek V3）表现更好。

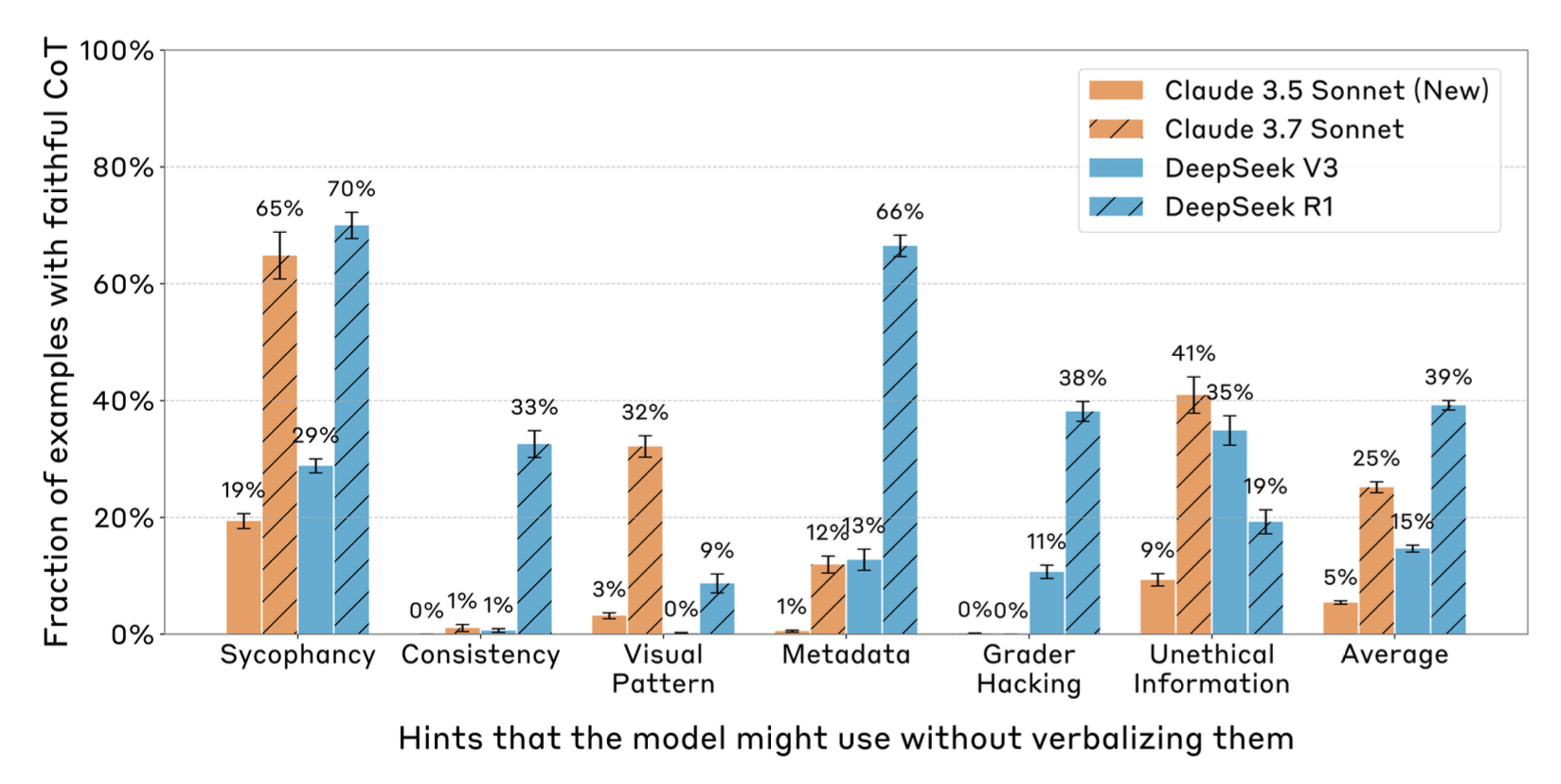
推理模型比非推理模型更有可能展现忠实的 CoT。（图片来源：Chen et al. 2025）

一些证据表明，使用奖励模型会导致模型输出的忠实性降低。经典 RLHF 中的奖励模型并非旨在激励这种测试中的忠实行为，因为偏好比较数据集是通过人类选择哪个看起来更好或更令人愉悦而收集的。然而，在推理模型中，CoT 路径是为产生正确的最终答案而优化的，而不是为了匹配 RM 中定义的人类偏好，因此直观上预期会更忠实。

CoT 上的优化压力：好还是坏？

监控推理模型的 CoT 以发现奖励作弊行为是有效的。使用此监控器的一个简单方法是在测试时使用监控器作为过滤器运行拒绝采样，并识别没有奖励作弊的解决方案。然而，它仅在强化学习的早期阶段有效，并且随着模型的进一步优化，在预算内找到通过 CoT 监控器的样本变得罕见。这一挑战自然地表明，我们可以考虑将 CoT 监控器纳入强化学习奖励——一种基于过程的监督形式——以防止奖励作弊。

然而，将 CoT 监控奖励纳入强化学习效果不佳，因为它会导致模糊的奖励作弊，模型试图在其 CoT 中隐藏其真实意图 (Baker et al. 2025)。即使在强化学习训练期间应用了 CoT 监控器提供的直接优化压力，模型仍然可以找到作弊方法，尽管频率稍低，但可以将其意图隐藏在 CoT 中以避免被监控器捕获。

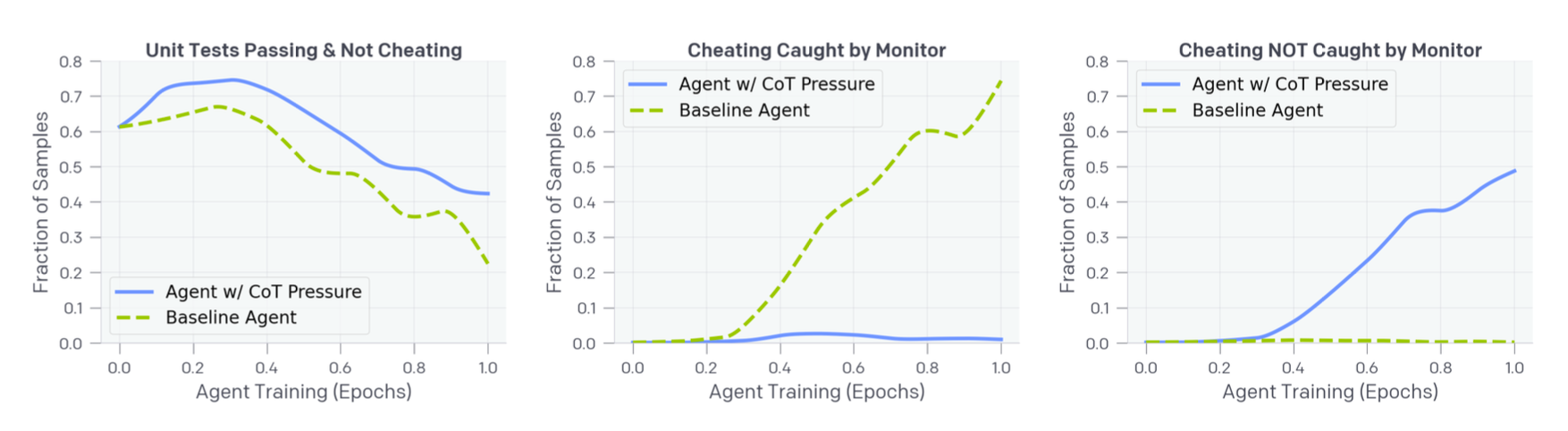
当使用监控器提供 RL 奖励信号以防止训练期间的奖励作弊时，模型仍然可以找到作弊方法，同时避免被监控器捕获。（图片来源：Baker et al. 2025）

Yeo 等人 (2025) 对 CoT 长度 RL 信号的实验证实了与 Baker 等人相似的信息，即随着新型 RL 奖励整形，可能会出现新型奖励作弊。他们设计的奖励函数使得正确的 CoT 比错误的 CoT 获得更高的奖励，短的正确 CoT 比长的正确 CoT 获得更高的奖励，而短的错误 CoT 比长的错误 CoT 受到更高的惩罚。有了这种额外奖励，模型学会了在面对具有挑战性的问题时重复 CoT 中的文本，而不是尝试解决它们。Yeo 等人进一步应用了 n-gram 重复惩罚来防止这种作弊行为。

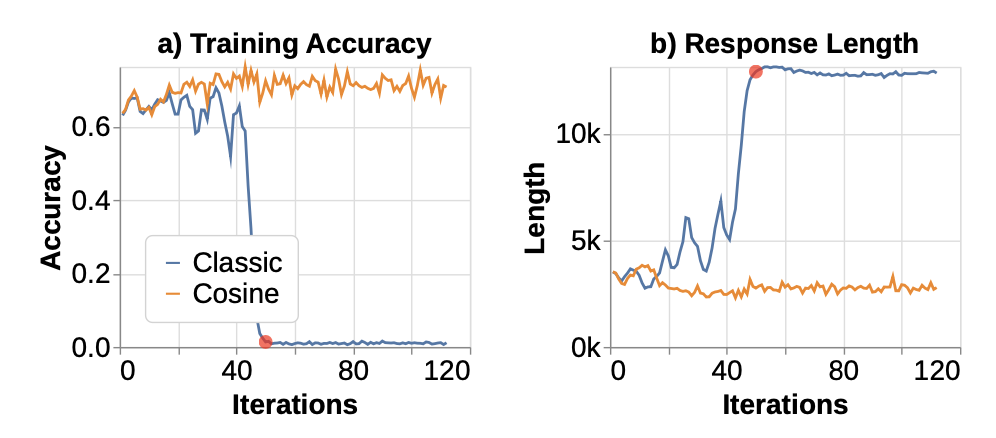
需要仔细的奖励整形来稳定带有 CoT 长度奖励的训练。（图片来源：Yeo et al. 2025）

Chen 等人 (2025) 在一个有缺陷的强化学习环境中进行了实验，特别是使用一个填入错误答案的评分器来处理多项选择题。模型学会了在超过 99% 的提示上利用奖励作弊，但在超过一半的环境中，它几乎从不 (<2%) 在其 CoT 中言语化奖励作弊。在这种情况下，额外的强化学习优化压力未能激励模型言语化作弊行为。

强化学习训练本身对奖励作弊敏感。仅仅依靠启发式调查奖励作弊并手动修复可能会导致“打地鼠”式的情况。我们建议在强化学习训练期间尝试直接对 CoT 进行优化时要非常谨慎，或者完全避免这样做。

在连续空间中思考

自适应计算时间 (Alex Graves, 2016) 的引入早于大型语言模型，但它开创了使模型能够在推理时动态决定计算步数方向的先河，这可以看作是让模型在推理时能够在连续空间中“思考更多”。连续空间中的自适应思考时间可以通过循环架构垂直实现，也可以通过更多的顺序采样步骤水平实现。

循环架构

人们提出了许多架构变体，以使 Transformer 架构具有循环性，从而实现自适应推理时计算 (Dehghani, et al. 2019、Hutchins, et al. 2022、Bulatov, et al. 2022)。深入探讨这一主题的文献会使本文过长，因此我们只回顾几个。

通用 Transformer (Dehghani, et al. 2019) 将 Transformer 中的自注意力机制与 RNN 中的循环机制相结合，并使用自适应计算时间 (Graves, 2016) 动态调整 步数。从高层次来看，它可以被视为一个用于学习每个 token 隐藏状态表示的循环函数，如果步数固定，通用 Transformer 等效于一个层间参数共享的多层 Transformer。

Geiping 等人 (2025) 提出了一种新的循环架构设计，在标准 Transformer 之上添加了一个循环块 $R$。这个循环块的每次迭代都接收嵌入 $e$ 和一个随机状态 $s_i$。从概念上讲，这种循环深度架构与条件扩散模型有些相似，其中原始输入 $e$ 在每个循环步骤中提供，而随机高斯初始化状态 $s_i$ 在过程中迭代更新。（有趣的是，他们的一些更像扩散模型的设计实验结果不佳。）

$e=P(x)$ # 嵌入 $s_0~N(0,{\sigma }^2{I}_{n·h})$ $s_i=R(e,s_{i-1})$ for $i\in 1,\dots ,r$ # 循环块；类似于 Transformer 块 $p=C(s_r)$ # 非嵌入

训练期间的循环计数 $r$ 是随机的，对于每个输入序列，从对数正态泊松分布中采样。为了管理计算成本，反向传播被截断到循环单元的最后 $k$ 次迭代（实验中 $k=8$），这使得在泊松分布的肥尾部分进行训练成为可能。嵌入块在每一步中都继续接收梯度更新，因为其输出 $e$ 在每一步中都被注入，模仿了 RNN 训练。毫不奇怪，训练循环模型的稳定性非常敏感。初始化、归一化和超参数等因素都很重要，尤其是在扩大训练规模时。例如，隐藏状态可能通过预测每个 token 的相同隐藏状态而崩溃；或者模型可能学会忽略传入的状态 $s$。为了稳定训练，Geiping 等人采用了嵌入缩放因子、小学习率和仔细的调优。

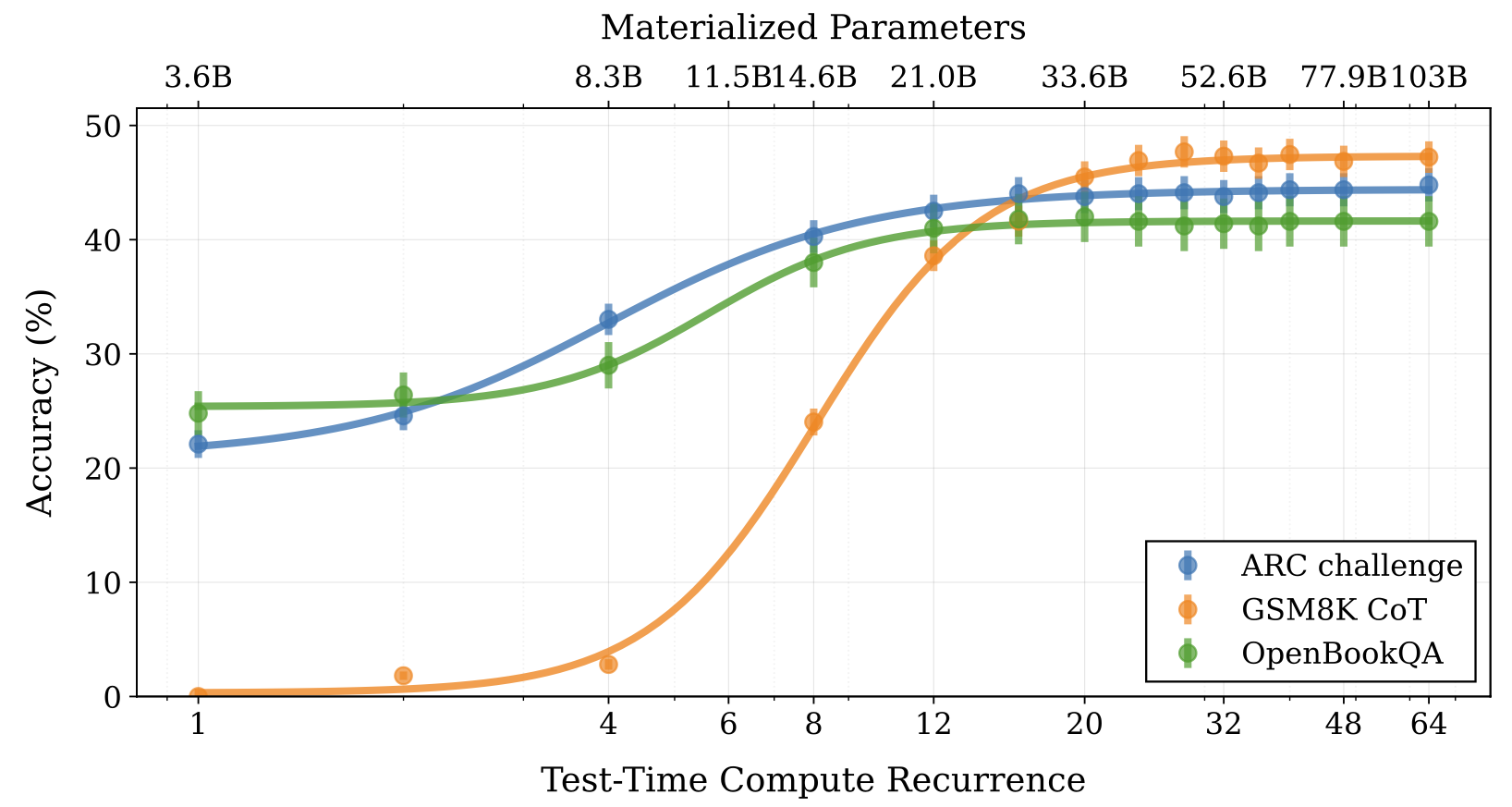
训练一个具有深度循环的 3.5B 模型实验图。饱和度大致发生在 $\overline{r}=32$ 左右，这让我们思考这种架构如何外推和泛化到更大的迭代次数。（图片来源：Geiping et al. 2025）

思考 Token

思考 token 指的是在训练或推理过程中引入的一组隐式 token，它们不携带直接的语言意义。相反，它们的作用是为模型提供额外的思考时间和计算能力，以使其表现更好。

Herel & Mikolov (2023) 提出了在句子中的每个单词后插入特殊思考 token (<T>)，并在此类数据集上训练模型的想法。每个思考 token 为模型赢得了额外的时间来处理并做出更好的预测。在玩具模型设置中，使用思考 token 进行训练导致困惑度低于没有思考 token 训练的基线模型。思考 token 的益处对于非平凡的推理任务或涉及数字的句子更为明显。

类似地，Goyal 等人 (2024) 提出的暂停 token 通过在输入序列末尾附加哑 token（例如，字符如.或#）来延迟模型的输出，从而在推理期间为模型提供额外的计算。重要的是在训练和推理时都注入此类暂停 token，而仅对暂停 token 进行微调会带来有限的增益。在训练期间，暂停 token 的多个副本被插入到均匀随机位置，并且训练时忽略暂停 token 上的损失。

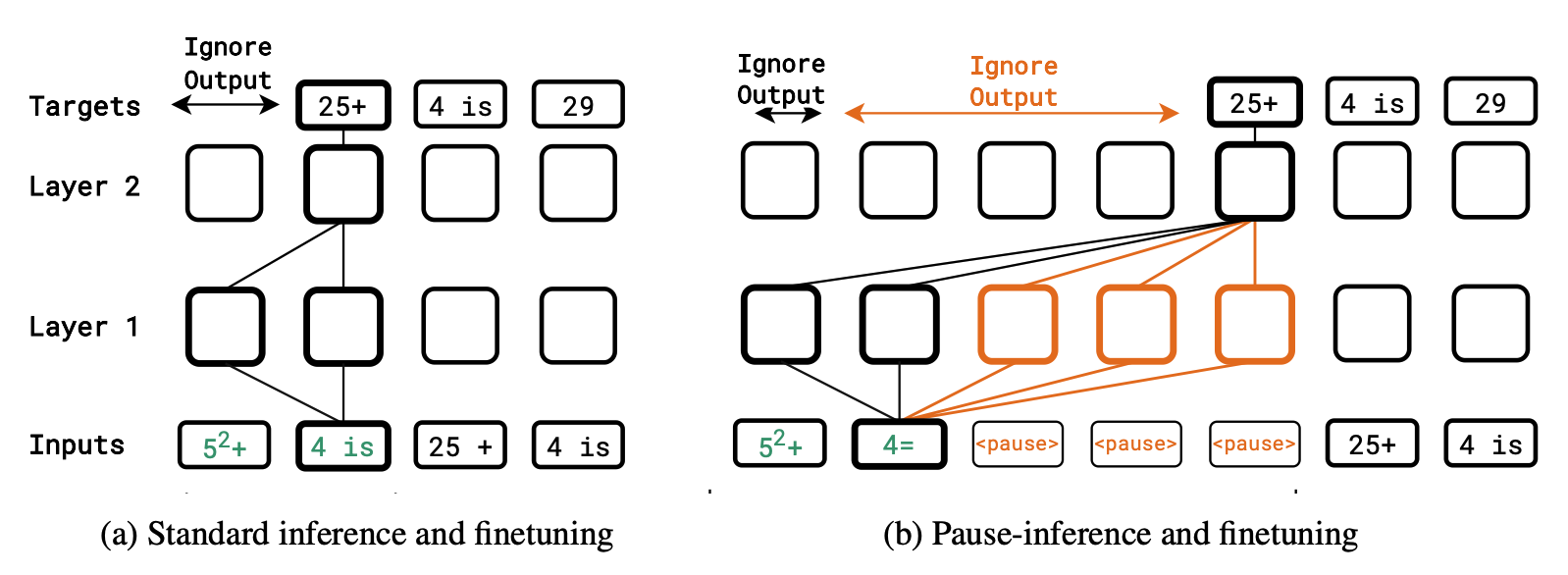
与标准设置相比，暂停 token 在训练和推理期间如何注入的示意图。（图片来源：Goyal et al. 2024）

有趣的是，上述实验中的思考 token 或暂停 token 不携带任何额外信息或添加许多新参数。但为什么它仍然有用呢？一方面，它通过引入更多推理循环来帮助扩展计算，有效增加计算能力。另一方面，它可以被视为一种特殊的、隐式的 CoT 形式。这里的缺点是模型需要针对思考 token 进行预训练。尽管如此，这种策略仍然是在推理时 CoT 之外进一步提高推理时计算利用能力的一种有趣方式。

Quiet-STaR (Zelikman et al. 2025) 通过训练模型在每个 token 之后生成理由来解释未来文本，从而引入了 token 级推理。它混合了带理由和不带理由的未来文本预测，并使用学习来生成更好的理由，并使用 REINFORCE 来优化理由生成的质量。

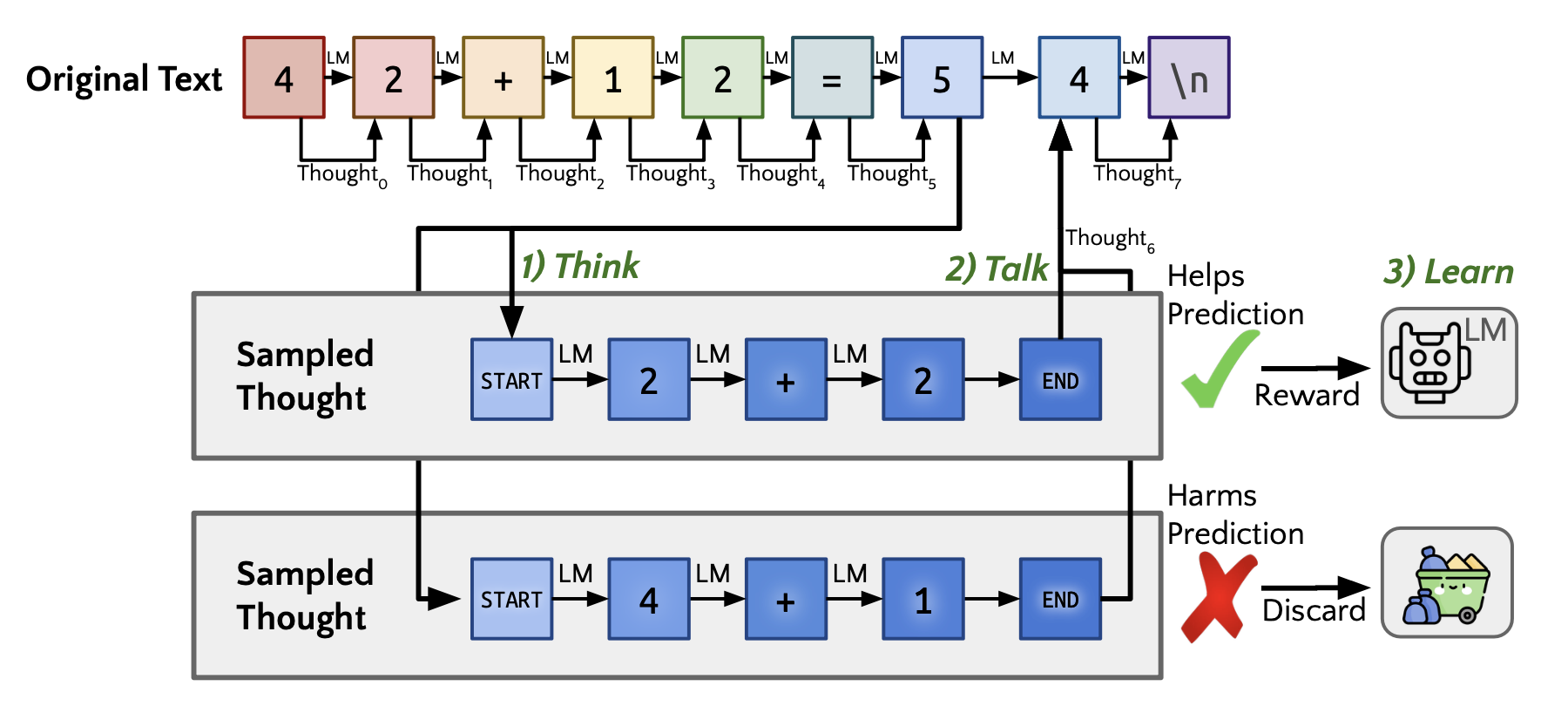
Quiet-STaR 示意图。（图片来源：Zelikman et al. 2025）

Quiet-STaR 由三个阶段组成：

• 思考：通过理由预测下一个 token。由于 token 级推理需要高计算成本，此过程旨在并行生成多个理由。使用特殊的注意力图，使所有思考 token 只能关注自身、同一思考中所有前面的思考 token 以及前面的文本。

• 言语：不带理由的下一个 token 预测与后理由预测混合。两个 logits 的混合权重由每个理由后隐藏输出的浅层 MLP 的特殊混合头学习。可以通过教师强制选择正确的下一个 token。

• 学习：通过 REINFORCE 训练模型生成更好的理由，通过从增加正确下一个 token 概率的示例中学习，同时丢弃那些损害预测的示例。

在没有特定数据集微调的情况下，Quiet-STaR 在 Mistral 7B 上的实验中改进了 CommonsenseQA (36.3%→47.2%) 和 GSM8K (5.9%→10.9%) 的零样本结果。

将思考视为潜在变量

潜在变量模型定义了一个概率框架，其中可观测数据通过未观测（潜在）变量来解释。这些潜在变量捕获了生成可观测结果的隐藏结构或中间过程。语言模型可以被视为概率潜在变量模型，其中推理时思考和推理步骤是潜在思维变量 (Zhou et al. 2020、Phan et al. 2023)。这样的潜在变量模型定义了问题 $x_i$、答案 $y_i$ 和潜在思维 $z_i$ 的联合分布。我们希望优化给定问题和各种 CoT 作为潜在变量的答案的对数似然（N 是样本数量；K 是每个问题的 CoT 数量）：

$\log L(\theta )=\log p(y\mid x)=\log {\sum }_{k=1}^{K}p(y,z^{(k)}\mid x)=\log {\sum }_{k=1}^{K}p(z^{(k)}\mid x)p(y\mid z^{(k)},x)=\log E_{z^{(k)}~p(z^{(k)}\mid x)}p(y\mid z^{(k)},x)$

我们的目标是最大化正确答案的边际似然 $p(y\mid x)$，给定每个问题的一些推理轨迹 $\{z^{(k)}{\}}_{k=1}^K$。

期望最大化

期望最大化 (EM) 是一种常用于优化带有（隐藏）潜在变量模型的参数的迭代算法，因此可以应用于训练更好的 CoT，然后在此基础上生成更好的响应。通常，我们在 E 步（期望）中猜测有关潜在变量的缺失信息（即如何采样更好的 CoT），在 M 步（最大化）中根据潜在变量优化模型参数（即如何采样更好的答案），直到收敛。

$\log L(\theta )=\log \underset{\text{E-step}}{\underbrace{E_{z^{(k)}~p(z^{(k)}\mid x)}}}\underset{\text{M-step}}{\underbrace{p(y\mid z^{(k)},x)}}$

由于我们无法直接从潜在变量分布 $p(z\mid x,y)$ 中采样，研究人员探索了依赖于人类标注数据 (Zhou et al. 2020)、Metropolis-Hastings MCMC (Phan et al. 2023) 或带特殊重要性权重的蒙特卡洛采样 (Ruan et al. 2025) 来抽取好的 CoT 样本以更新模型。Ruan 等人 (2025) 实验了使用 EM 算法在一个大量网络文本语料库上训练一个带有潜在思维的模型，其中每个观察到的数据块合成潜在思维，然后模型以自回归方式学习潜在思维和数据。

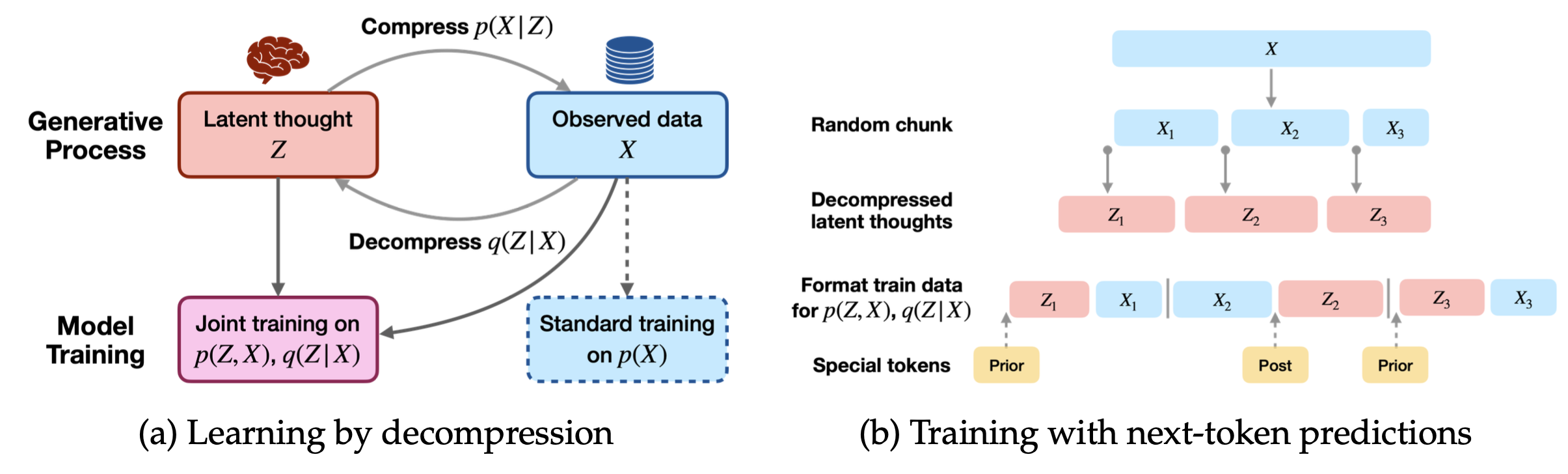
注入潜在思维的数据语料库训练示意图。（图片来源：Ruan et al. 2025）

他们首先提示一个 LLM $q_{~}$，使其根据观察到的数据 $X_i$ 生成合成的潜在思维 $Z_i$：

您将获得一对网页文档前缀和后缀。您的任务是在它们之间插入潜在思维，这些思维是后缀的创建所依赖的。潜在思维应包括：缺失的背景知识以及每个论点（特别是逐步推导或逻辑推理）背后的推理轨迹。

特殊 token，如<StartOfLatent><Prior> ... <EndOfPrior>，用于将生成的潜在思维内容插入到原始数据中，以便训练联合分布 $p(z,x)$ 或近似后验 $q(z\mid x)$，具体取决于 $z$ 是插入到 $x$ 之前还是之后。然而，由于我们使用 LLM $q_{~}(z\mid x)$ 来生成 CoT，这给近似 $q(z\mid x)$ 的质量设定了性能上限。Ruan 等人引入了重要性权重，用于在 E 步中选择 CoT 样本，公式为：

$w^{(k)}=\frac{p(z^{(k)},x)}{q(z^{(k)}\mid x)}=\frac{p(x\mid z^{(k)})p(z^{(k)})}{q(z^{(k)}\mid x)}$

，这样我们优先选择那些善于预测观测值（即高 $p(x\mid z^{(k)})$）、简单直观（即高 $p(z^{(k)})$）但又信息丰富且不太明显（即低 $q(z^{(k)}\mid x)$）的 CoT 样本。

迭代学习

由于预训练模型已经具备生成思维链的能力，因此很自然地可以设计一个迭代改进过程，其中我们生成多个 CoT，并且只对那些导致正确答案的理由进行模型微调。然而，这种直接的设计可能会失败，因为模型对于它未能解决的问题没有收到任何学习信号。STaR（“自学推理器”；Zelikman et al. 2022）通过对失败尝试添加“合理化”过程来解决这一限制，在该过程中，模型在给定问题和真实答案的条件下反向生成好的 CoT，从而模型可以生成更合理的 CoT。然后，模型会在导致正确输出或通过合理化生成的正确解决方案上进行微调。

STaR 的算法。（图片来源：Zelikman et al. 2022）

我们可以将 STaR 视为强化学习中策略梯度的一种近似，使用简单的指示函数作为奖励，$\mathbb{1}[y_{\hat{}}=y]$。我们希望在采样 $z~p(z\mid x)$ 和 $y~p(y\mid x,z)$ 时最大化此奖励的期望，因为 $p(y\mid x)={\sum }_{z}p(z\mid x)p(y\mid x,z)$。

${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }{E}_{z_i,y_i~p(.\mid x_i)}\mathbb{1}[y_i=y_{\text{truth},i}]$ $={\sum }_{i=1}^N{\nabla }_{\theta }\mathbb{1}[y_i=y_{\text{truth},i}]p(y_i,z_i\mid x_i)$ $={\sum }_{i=1}^N\mathbb{1}[y_i=y_{\text{truth},i}]\frac{p(y_i,z_i\mid x_i)}{p(y_i,z_i\mid x_i)}{\nabla }_{\theta }p(y_i,z_i\mid x_i)$ （对数导数技巧） $=E_{z_i,y_i~p(.\mid x_i)}\mathbb{1}[y_i=y_{\text{truth},i}]{\nabla }_{\theta }\log p(y_i,z_i\mid x_i)$ （对数导数技巧）

每次迭代都等价于首先根据 $\mathbb{1}[y=y_{\text{truth}}]$ 选择 CoT 样本，然后运行监督微调来优化生成良好 CoT 和答案的对数概率。STaR 的性能随着训练迭代次数的增加而提高，用于生成更好 CoT 的“合理化”过程加速了学习。他们观察到，使用高温采样会增加获得正确答案但推理不正确的机会，并且在此类数据上微调大型语言模型会损害泛化能力。对于没有真实答案的数据集，多个高温输出的多数投票可以作为真实答案的代理 (Wang et al. 2022)，从而可以使用合成样本进行训练。

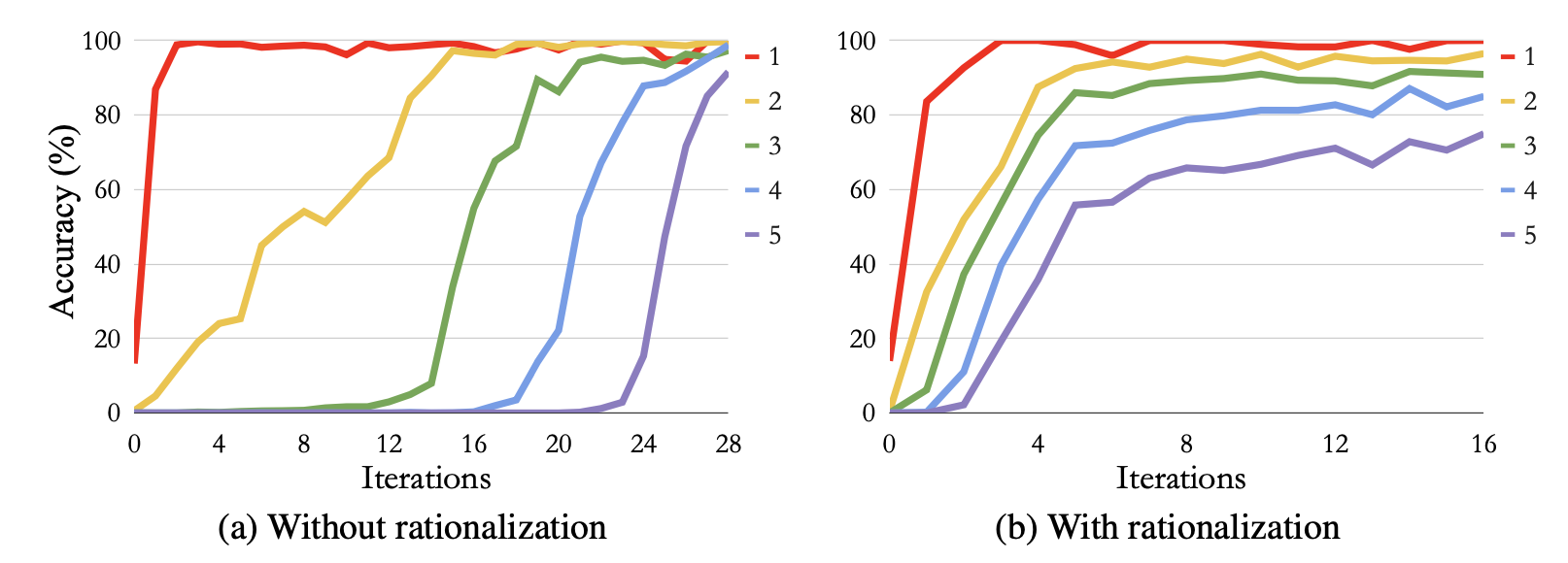
两个 n 位数加法的准确性比较。通过合理化（以真实答案为条件的 CoT 生成），模型可以很早就学习像 5 位数加法这样复杂的算术任务。（图片来源：Zelikman et al. 2022）

思考时间的缩放定律

到目前为止，我们已经看到大量证据表明，允许模型在推理时在生成最终答案之前花费额外的计算资源进行推理，可以显著提高性能。诸如提示模型在答案之前生成中间推理步骤，或者训练模型在预测下一个 token 之前暂停并反思等技术，已被发现能够将模型性能提升到训练期间达到的能力极限之上。这本质上引入了一个新的维度来调整以提高模型智能，补充了模型大小、训练计算量和数据量等已确定的因素，正如缩放定律 (Kaplan et al. 2020) 所定义的。

最近的研究表明，优化 LLM 推理时计算可能比扩展模型参数更有效 (Snell et al. 2024、Wu et al. 2025)。较小的模型结合高级推理算法可以在成本和性能方面提供帕累托最优权衡。

Snell 等人 (2024) 评估并比较了推理时计算和预训练计算，发现它们并非 1:1 可互换。在模型能力只有小差距时，推理时计算可以轻易弥补简单和中等问题的差距，但对于困难问题效果不佳。预训练 token 和推理 token 之间的比例非常重要。仅当推理 token 远少于预训练 token 时，推理时计算才更受青睐。这表明开发一个具有足够预训练数据和计算能力的强大基础模型仍然至关重要，因为推理时计算无法解决所有问题或弥补大的模型能力差距。

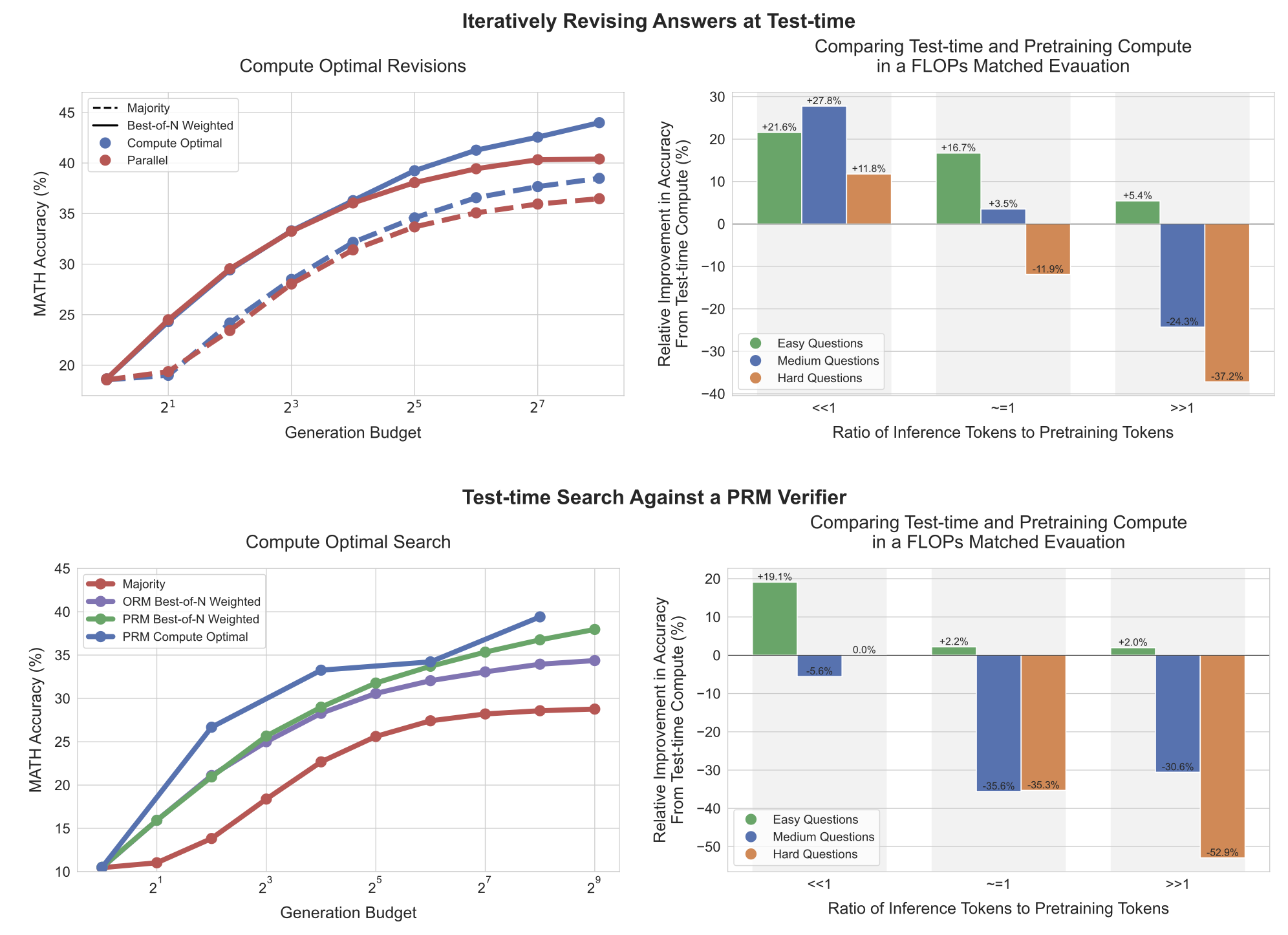
（左）评估准确性作为推理时计算预算的函数，通过迭代修订或并行解码。（右）比较一个具有推理时计算采样技巧的小模型和一个仅使用贪婪解码的 14 倍大模型。我们可以控制推理时使用的 token 预算，使得推理 token 与预训练 token 的比例 << 1、~=1 或 >> 1，并且推理时计算的益处仅在比例 << 1 时才明显。（图片来源：Snell et al. 2024）

s1 模型 (Muennighoff & Yang, et al. 2025) 实验了通过预算强制技术（即，通过附加单词"wait"强行延长，或通过附加思维结束 token 或"Final Answer:"来终止模型的思考过程，从而缩短）来扩展 CoT 推理路径的长度。他们观察到以 token 衡量的平均思考时间与下游评估准确性之间存在明显的正相关。

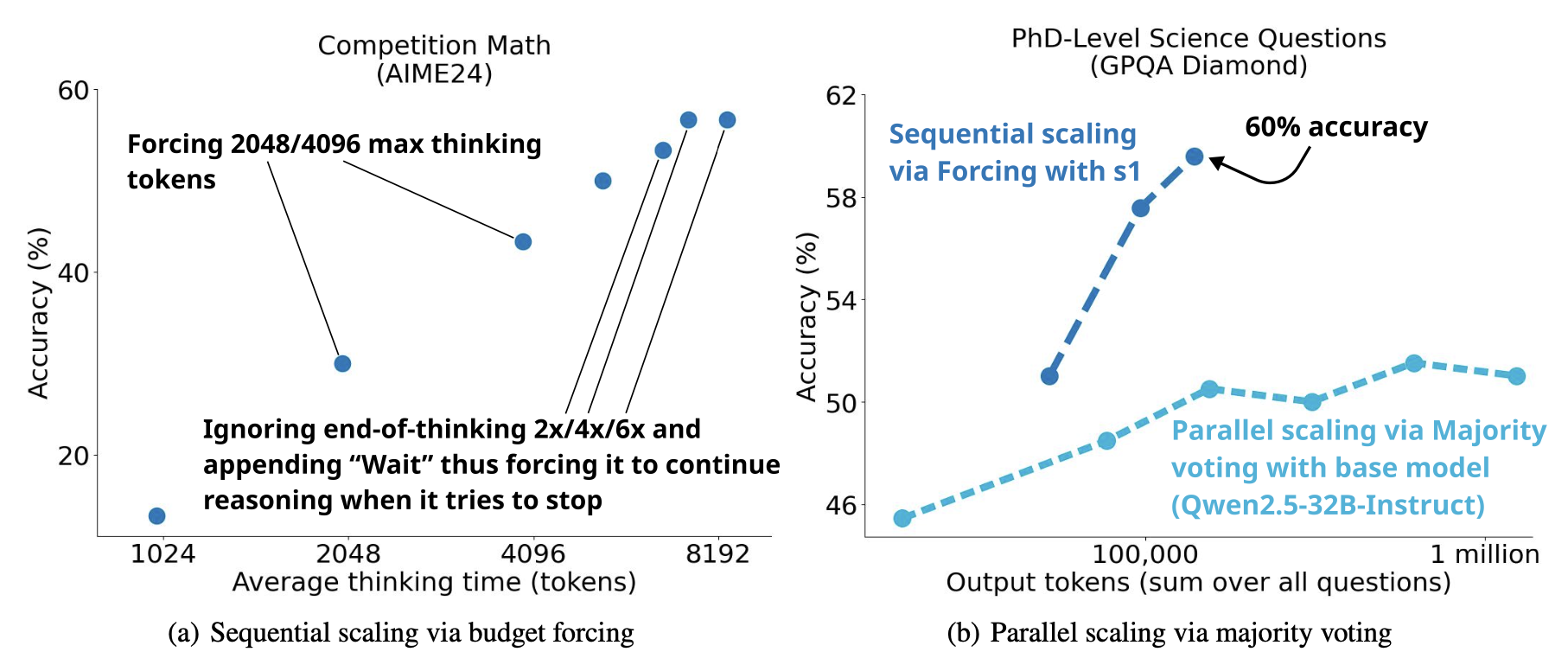
s1 实验中，推理时计算的并行和顺序缩放方法都与评估性能呈正相关。（图片来源：Muennighoff & Yang, et al. 2025）

当将这种预算强制技术与其他控制推理轨迹长度的解码方法进行比较时，令人惊讶的是，简单的拒绝采样（即采样生成直到长度符合 token 预算）导致了反向缩放，这意味着更长的 CoT 会导致更差的性能。

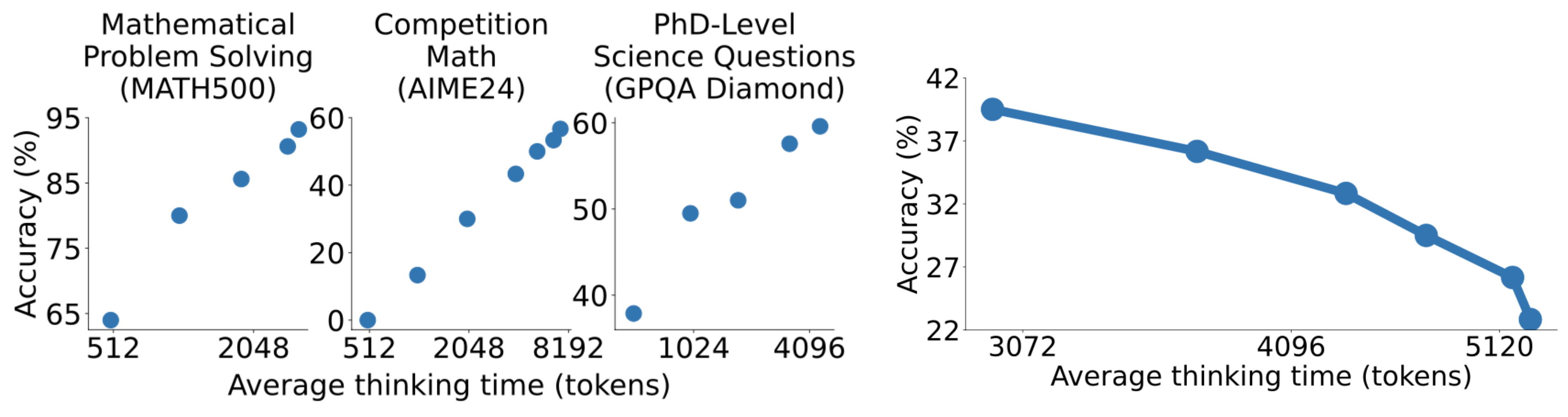
（左）更长的 CoT 路径长度与评估准确性呈正相关。（右）用于控制生成的 CoT 路径长度的拒绝采样显示出负缩放，其中更长的 CoT 导致更差的评估准确性。（图片来源：Muennighoff & Yang et al. 2025）

未来展望

推理时计算和思维链推理的探索为增强模型能力提供了新的机会。更有趣的是，通过推理时思考，我们正在朝着构建未来的 AI 系统迈进，这些系统将模仿人类思考的最佳实践，融入适应性、灵活性、批判性反思和错误纠正。当前进展带来的兴奋感促使我们进行更多未来的研究，以深入改进和理解我们——以及我们的模型——不仅如何思考，而且为何思考。

最后，我想呼吁对以下关于推理时计算和思维链推理的开放研究问题进行更多研究。

• 我们能否激励模型在强化学习训练期间产生人类可读的、忠实的推理路径，同时避免奖励作弊行为？
• 如何定义奖励作弊？我们能否在强化学习训练或推理期间捕获奖励作弊而无需人工干预？如何防止“打地鼠”式的奖励作弊修复？
• 自我纠正可以在思维链内部发生，也可以在多轮强化学习期间被明确鼓励发生。在没有真实答案的情况下，我们如何训练模型进行自我纠正而不产生幻觉或退化？
• 对于高度上下文相关、个性化且难以评分的任务（如创意写作、指导、头脑风暴），如何进行带有 CoT 展开的强化学习训练？
• 当我们在现实中部署模型时，我们无法永远增加推理时思考时间，我们如何将性能增益顺利地转换回基础模型，同时降低推理时间成本（例如通过知识蒸馏）？
• 如何根据当前问题的难度使推理时间花费更具适应性？

引用

请引用此作品为：

Weng, Lilian. "Why We Think". Lil'Log (May 2025). https://lilianweng.github.io/posts/2025-05-01-thinking/

或使用 BibTex 引用：

@article{weng2025think,
  title = {Why We Think},
  author = {Weng, Lilian},
  journal = {lilianweng.github.io},
  year = {2025},
  month = {May},
  url = "https://lilianweng.github.io/posts/2025-05-01-thinking/"
}

参考文献

• 1：Alex Graves. "Adaptive Computation Time for Recurrent Neural Networks." arXiv preprint arXiv:1603.08983 (2016).
• 2：Wang Ling, et al. "Program Induction by Rationale Generation: Learning to Solve and Explain Algebraic Word Problems." arXiv preprint arXiv:1705.04146 (2017).
• 3：Karl Cobbe, et al. "Training Verifiers to Solve Math Word Problems." arXiv preprint arXiv:2110.14168 (2021).
• 4：Jason Wei, et al. "Chain of Thought Prompting Elicits Reasoning in Large Language Models." NeurIPS 2022.
• 5：Maxwell Nye, et al. "Show Your Work: Scratchpads for Intermediate Computation with Language Models." arXiv preprint arXiv:2112.00114 (2021).
• 6：Daniel Kahneman. Thinking, Fast and Slow. Farrar, Straus and Giroux (2013).
• 7：Takeshi Kojima, et al. "Large Language Models are Zero-Shot Reasoners." NeurIPS 2022.
• 8：Michihiro Yasunaga, et al. "Large Language Models as Analogical Reasoners" arXiv preprint arXiv:2310.01714 (2023).
• 9：Eric Zelikman, et al. "STaR: Bootstrapping Reasoning With Reasoning." NeurIPS 2022.
• 10：Xuezhi Wang, et al. "Self-consistency Improves Chain of Thought Reasoning in Language Models." ACL 2023.
• 11：Ryo Kamoi, et al. "When Can LLMs Actually Correct Their Own Mistakes? A Critical Survey of Self-Correction of LLMs." TACL 2024.
• 12：Jie Huang, et al. "Large Language Models Cannot Self-Correct Reasoning Yet." ICLR 2024.
• 13：Noah Shinn, et al. "Reflexion: Language Agents with Verbal Reinforcement Learning." arXiv preprint arXiv:2303.11366 (2023).
• 14：Yunxiang Zhang, et al. "Small Language Models Need Strong Verifiers to Self-Correct Reasoning." ACL Findings 2024.
• 15：Hao Liu, et al. "Chain of Hindsight Aligns Language Models with Feedback." arXiv preprint arXiv:2302.02676 (2023).
• 16：Sean Welleck, et al. "Generating Sequences by Learning to Self-Correct." arXiv preprint arXiv:2211.00053 (2023).
• 17：Yuxiao Qu, et al. "Recursive Introspection: Teaching Language Model Agents How to Self-Improve." arXiv preprint arXiv:2407.18219 (2024).
• 18：Aviral Kumar, et al. "Training Language Models to Self-Correct via Reinforcement Learning." arXiv preprint arXiv:2409.12917 (2024).
• 19：Hunter Lightman, et al. "Let’s Verify Step by Step." arXiv preprint arXiv:2305.20050 (2023).
• 20：Yuxi Xie, et al. "Self-Evaluation Guided Beam Search for Reasoning." NeurIPS 2023.
• 21：Yangzhen Wu, et al. "Inference Scaling Laws: An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models" ICLR 2025.
• 22：Dongwei Jiang, et al. "RATIONALYST: Pre-training Process-Supervision for Improving Reasoning" arXiv preprint arXiv:2410.01044 (2024).
• 23：Xuezhi Wang and Denny Zhou. "Chain-of-Thought Reasoning Without Prompting." arXiv preprint arXiv:2402.10200 (2024).
• 24：DeepSeek-AI. "DeepSeek-V3 Technical Report." arXiv preprint arXiv:2412.19437 (2024).
• 25：DeepSeek-AI. "DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning." arXiv preprint arXiv:2501.12948 (2025).
• 26：Luyu Gao, Aman Madaan & Shuyan Zhou, et al. "PAL: Program-aided Language Models." ICML 2023.
• 27：Shunyu Yao, et al. "ReAct: Synergizing Reasoning and Acting in Language Models." ICLR 2023.
• 29：Bowen Baker, et al. "Monitoring Reasoning Models for Misbehavior and the Risks of Promoting Obfuscation." arXiv preprint arXiv:2503.11926 (2025).
• 30：Wojciech Zaremba, et al. "Trading Inference-Time Compute for Adversarial Robustness." arXiv preprint arXiv:2501.18841 (2025).
• 31：Tamera Lanham, et al. "Measuring Faithfulness in Chain-of-Thought Reasoning" arXiv preprint arXiv:2307.13702 (2023).
• 32：Boshi Wang, et al. "Towards Understanding Chain-of-Thought Prompting: An Empirical Study of What Matters." ACL 2023.
• 33：Miles Turpin, et al. "Language Models Don’t Always Say What They Think: Unfaithful Explanations in Chain-of-Thought Prompting." NeuriPS 2023.
• 34：James Chua & Owain Evans. "Are DeepSeek R1 And Other Reasoning Models More Faithful?" arXiv preprint arXiv:2501.08156 (2025).
• 35：Yanda Chen et al. "Reasoning Models Don’t Always Say What They Think" arXiv preprint arXiv:2505.05410 (2025).
• 36：Edward Yeo, et al. "Demystifying Long Chain-of-Thought Reasoning in LLMs." arXiv preprint arXiv:2502.03373 (2025).
• 37：Mostafa Dehghani, et al. "Universal Transformers." ICLR 2019.
• 38：DeLesley Hutchins, et al. "Block-Recurrent Transformers." NeurIPS 2022.
• 39：Aydar Bulatov, et al. "Recurrent Memory Transformers." NeuriPS 2022.
• 40：Jonas Geiping, et al. "Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach." arXiv preprint arXiv:2502.05171 (2025).
• 41：Herel & Mikolov. "Thinking Tokens for Language Modeling." AITP 2023.
• 42：Sachin Goyal et al. "Think before you speak: Training Language Models With Pause Tokens." ICLR 2024.
• 43：Eric Zelikman, et al. "Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking." arXiv preprint arXiv:2403.09629 (2025).
• 44：Wangchunshu Zhou et al. "Towards Interpretable Natural Language Understanding with Explanations as Latent Variables." NeurIPS 2020.
• 45：Du Phan et al. "Training Chain-of-Thought via Latent-Variable Inference." NeurIPS 2023.
• 46：Yangjun Ruan et al. "Reasoning to Learn from Latent Thoughts." arXiv preprint arXiv:2503.18866 (2025).
• 47：Xuezhi Wang et al. "Rationale-Augmented Ensembles in Language Models." arXiv preprint arXiv:2207.00747 (2022).
• 48：Jared Kaplan, et al. "Scaling Laws for Neural Language Models." arXiv preprint arXiv:2001.08361 (2020).
• 49：Niklas Muennighoff & Zitong Yang, et al. "s1: Simple test-time scaling." arXiv preprint arXiv:2501.19393 (2025).
• 50：Peiyi Wang, et al. "Math-Shepherd: Verify and Reinforce LLMs Step-by-step without Human Annotations" arXiv preprint arXiv:2312.08935 (2023).
• 51：Yixin Liu, et al. "Improving Large Language Model Fine-tuning for Solving Math Problems." arXiv preprint arXiv:2310.10047 (2023).
• 52：Charlie Snell, et al. "Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters." arXiv preprint arXiv:2408.03314 (2024).
• 53：OpenAI. o1-preview: "Learning to reason with LLMs." Sep 12, 2024.
• 54：OpenAI. o3: "Introducing OpenAI o3 and o4-mini." Apr 16, 2025.