亨利·庞加莱 (Henri Poincaré)-不耐烦的天才(第一部分)

30 Apr, 2025

作者：费迪南德·维尔hulst (Ferdinand Verhulst)

费迪南德·维尔hulst
数学研究所 (Mathematisch Instituut)
乌得勒支大学 (University of Utrecht)
Budapestlaan 6
乌得勒支 (Utrecht)
荷兰 (Netherlands)

ISBN 978-1-4614-2406-2 ISBN 978-1-4614-2407-9 (电子书 eBook)
DOI 10.1007/978-1-4614-2407-9
斯普林格 (Springer) 纽约 海德堡 多德雷赫特 伦敦

美国国会图书馆控制号 (Library of Congress Control Number): 2012937853

数学学科分类 (Mathematics Subject Classification) (2010): 01A55, 01A70, 03-03, 11F99, 34-03, 35-03, 37-03, 70-03 $\circledcirc$ 斯普林格科学+商业媒体纽约 2012 (Springer Science+Business Media New York 2012)

本作品受版权保护。出版商保留所有权利，无论是全部还是部分材料，特别是翻译权、重印权、插图再利用权、朗诵权、广播权、缩微胶片或其他任何物理方式的复制权、以及信息存储和检索、电子改编、计算机软件或通过现在已知或将来开发的类似或不同方法的传播权。与评论或学术分析相关的简短摘录，或专门为输入和在计算机系统上执行而提供的材料，供作品购买者专用的，不受此法律保留的限制。本出版物或其部分的复制只有在符合出版商所在地当前版本的版权法 (Copyright Law) 规定下才被允许，并且必须始终获得斯普林格 (Springer) 的使用许可。使用许可可以通过版权结算中心 (Copyright Clearance Center) 的 RightsLink 获取。违规者将根据相应的版权法受到起诉。

在本出版物中使用通用描述性名称、注册名称、商标 (trademarks)、服务标记 (service marks) 等，即使没有具体说明，也不意味着这些名称不受相关保护性法律法规的约束，因此可供一般使用。

虽然本书中的建议和信息在出版之日被认为是真实和准确的，但作者、编辑或出版商均不对可能出现的任何错误或遗漏承担任何法律责任。出版商对本书所含材料不作任何明示或暗示的保证。

使用无酸纸印刷

斯普林格是斯普林格科学+商业媒体 (Springer Science+Business Media) 的一部分 (www.springer.com)

Voor Claartje A.

许多从未有机会了解什么是数学 (mathematics) 的人，将其与算术 (arithmetic) 混淆，并认为它是一门枯燥乏味的科学 (science)。然而，实际上，它是一门最需要想象力 (imagination) 的科学。在我看来，诗人 (poet) 必须看到别人看不到的东西，必须比别人看得更深。而数学家 (mathematician) 也必须做同样的事情。

——索尼娅·科瓦列夫斯卡娅 (Sonya Kovalevskaya)

前言

为一位在如此众多领域做出基础性贡献的科学家写传记 (biography) 是一项相当艰巨的任务。在这本传记上工作了几年后，我对一位德国 (German) 同事兼朋友说：“我必须停下来；庞加莱对我来说太伟大了。”在我看来，一个数学家不可能全面记述庞加莱所取得的一切成就。我的朋友回答说：“这不是放弃的好理由。庞加莱对我们所有人来说都太伟大了。”那种不可能的感觉并未消失，但我朋友的话是一种支持，我继续了下去。

还有一个障碍。庞加莱是一位探险家和冒险家，但他探索的是精神的丛林、沙漠和山脉。他进行了奇妙的旅行，但所有这些冒险都发生在他的头脑中。这样一个激动人心的生平，从外部看起来却如此平淡，该如何描述呢？在我沉浸于他的工作的那些日子里，有些时候我兴奋得几乎无法入睡。我希望读者也能同样被这些思想的冒险所吸引。

本书的若干章节的手稿曾被阅读和评论。我要感谢扬·阿尔茨 (Jan Aarts)、亨克·布劳尔 (Henk Broer)、勒洛夫·布鲁格曼 (Roelof Bruggeman)、迪尔克·范·达伦 (Dirk van Dalen)、安东尼奥·德加斯佩里斯 (Antonio Degasperis)、朱塞佩·加埃塔 (Giuseppe Gaeta)、让-马克·吉努 (Jean-Marc Ginoux)、金·普洛夫克 (Kim Plovker)、朱塞佩·普卡科 (Giuseppe Pucacco)、特奥·鲁伊格罗克 (Theo Ruijgrok) 和阿尔扬·塞文斯特 (Arjen Sevenster) 的评论。

特别感谢大卫·克莱默 (David Kramer)，他对本书进行了文字编辑，并通过一系列寻求澄清的疑问帮助提高了表述的清晰度。

从法语 (French) 和德语到英语的翻译由我负责，除了关于奥斯卡二世 (Oscar II) 获奖论文的第五章 (Chapter 5)，我使用了琼·巴罗-格林 [Barrow-Green 1997] (June Barrow-Green [Barrow-Green 1997]) 的优美著作。关于庞加莱与米塔-列夫勒 (Mittag-Leffler) 关系的第4.4节 (Section 4.4)，由菲利普·纳邦南 (Philippe Nabonnand) 编辑并附有许多宝贵注释的专著 [Poincaré 1999] (monograph [Poincaré 1999]) 提供了很大帮助。最后，谨对南锡庞加莱档案馆 (Nancy Poincaré Archive) 的网站和帮助表示感谢。

乌得勒支大学，2012

# 第一部分 亨利·庞加莱的一生

## 1 早年岁月：1854–1870
    1.1 童年，1854–1860
    1.2 学生时代：1860–1870
    1.3 中学与大学之间：1871–1873

# 2 大学教育：1873–1879
    2.1 艰难的一年
    2.2 在巴黎综合理工学院 (École Polytechnique) 的第二年
    2.3 矿业学院 (L’École des Mines)
    2.4 数学学位论文 (Dissertation in Mathematics)

# 3 在沃苏勒 (Vesoul) 和卡昂 (Caen) 取得的卓越成就
    3.1 在沃苏勒担任矿业工程师
    3.2 在卡昂担任讲师
    3.3 自守函数 (Automorphic Functions)：与富克斯 (Fuchs) 和克莱因 (Klein) 的联系

# 4 在巴黎 (Paris) 的职业生涯
    4.1 科研生涯概览
    4.2 交往与旅行
    4.3 保罗·阿佩尔 (Paul Appell)
    4.4 与米塔-列夫勒的联系
    4.5 讲义与学生
    4.6 法英风格之争
    4.7 相对论 (Relativity)：新力学
    4.8 社会参与

# 5 奥斯卡二世奖竞赛
    5.1 克罗内克 (Kronecker) 的评论与竞赛的开始
    5.2 委员会的活动与结论
    5.3 塞翁失马，焉知非福
    5.4 获奖论文

# 6 哲学与随笔
    6.1 最后的文集：科学机会主义
    6.2 几何学基础与数学思维
    6.3 关于数学与数学家
    6.4 自然科学原理
    6.5 数学物理 (Mathematical Physics) 笔记

# 7 终其一生，他是怎样一个人？

# 第二部分 科学细节与文献

# 8 自守函数
    8.1 从微分方程 (Differential Equations) 到自守函数
    8.2 菲利克斯·克莱因关于微分方程的讲座

# 9 微分方程与动力系统 (Dynamical Systems)
    9.1 庞加莱1879年的论文
    9.2 关于微分方程的革命性论文，1881–1882
    9.3 天体力学新方法 (Les Méthodes Nouvelles de la Mécanique Céleste)
    9.4 霍普夫分岔 (Hopf Bifurcation) 与自激振荡
    9.5 庞加莱-伯克霍夫定理 (Poincaré–Birkhoff Theorem)

## 10 位相分析 (Analysis Situs)
    10.1 早期拓扑学 (Topology)
    10.2 位相分析系列论文
    10.3 庞加莱猜想 (Poincaré Conjecture)

## 11 数学物理
    11.1 偏微分方程 (Partial Differential Equations)
    11.2 旋转流体质量 (Rotating Fluid Masses)
    11.3 电子动力学 (Dynamics of the Electron)：庞加莱群 (Poincaré Group) 与相对论
    11.4 在哥廷根 (Göttingen) 的六次讲座：1909年（相对论）
    11.5 宇宙起源学 (Cosmogony)

## 12 庞加莱在道德教育协会 (Society for Moral Education) 的演讲

## 13 历史数据与生平细节

# 参考文献 (References)

# 索引 (Index)

序幕

一个阳光明媚的下午，在法国 (French) 洛林省 (Lorraine) 南锡市 (Nancy) 的郊外，一位妇女正带着她的孩子亨利 (Henri) 和阿琳 (Aline) 散步。他们沿着一条两岸有小路的小溪走着，小路之间有几座桥相连。比妹妹大两岁的小亨利常常带着他的狗汤姆 (Tom) 跑在前面。突然，他发现母亲和妹妹已经过了河，正在对岸走着。亨利的母亲向他示意，他可以在下一座桥过河，但他立刻跳进了齐腰深的水里，冲过河去与母亲和妹妹会合。

这种解决问题的直接方式，是亨利·庞加莱余生的典型特征。还有那份不耐烦。

第一部分亨利·庞加莱的一生

第一章早年岁月

朱尔-亨利·庞加莱 (Jules-Henri Poincaré)，通常被称为亨利 (Henri)，1854年出生于南锡 (Nancy)，洛林公国 (duchy of Lorraine) 的首府，该地于1766年并入法国 (France)。他于1912年在巴黎 (Paris) 逝世，享年58岁，死于一次手术后的并发症。

1.1 童年，1854–1860

亨利的父亲，莱昂·庞加莱 (Léon Poincaré)，是一位对神经病学 (neurology) 特别感兴趣的医生。他是南锡大学 (University of Nancy) 的医学教授。他的母亲，欧仁妮·洛努瓦 (Eugénie Launois)，来自洛林省摩泽尔地区 (Moselle region) 的阿朗西 (Arrancy) 镇一个富裕的家庭。她是一位活泼聪慧的女性，也是一位体贴的妻子和慈爱的母亲，养育了两个孩子，亨利和阿琳 (Aline)（图1.3）。一生中，她都与孩子们保持着非常亲密的关系。下面是简要的洛努瓦 (Launois) 家族树示意图：

亨利的祖父，雅克-尼古拉·庞加莱 (Jacques-Nicolas Poincaré)，即莱昂的父亲，最初来自洛林的讷沙托 (Neufchâteau)。1820年，他在南锡定居，成为一名药剂师 (pharmacist)，并于1833年买下了一座名为马蒂尼公馆 (Hôtel Martigny) 的大房子。这座房子既是住所也是营业场所，因为建筑的一部分早先已被改建成了药房 (pharmacy)。它位于吉斯街 (Rue de Guise) 的街角，当时被称为老城街 (Rue de la Ville-Vieille)，见图1.1。这里成了亨利、阿琳及其父母、祖父母和其他亲戚的家。家里还有一位女佣菲菲娜 (Fifine)，她照看孩子们，给他们讲故事，教他们唱歌。后来，当阿琳嫁给哲学家埃米尔·布特鲁 (Émile Boutroux) 时，菲菲娜随他们搬到了巴黎。下面是简化的庞加莱 (Poincaré) 家族树示意图：

图1.1 亨利·庞加莱出生的房子

这座房子位于老城中心，离公爵宫 (ducal palace) 不远，至今仍矗立在那里。房子里有许多角落和楼梯，一个花园，以及其他可以玩耍和捉迷藏的地方，这个家激发了孩子们的想象力。祖父雅克-尼古拉经营药房直到1865年去世。后来，南锡大学将庞加莱的家改建为数学与物理研究所 (Institute of Mathematics and Physics)。建筑上的一块牌匾写着如下文字：

图1.2 莱昂·庞加莱和欧仁妮·洛努瓦，亨利和阿琳的父母

在这座房子里，亨利·庞加莱于1854年4月29日出生。他是法兰西学术院 (Académie Française) 和法国科学院 (Académie des Sciences) 的成员。他于1912年7月17日在巴黎逝世。

亨利和阿琳成长在一个我们现在称之为扩展家庭 (extended family) 的环境中。他们的父亲总是忙于病人和研究，但母亲给了他们充足的关爱（莱昂和欧仁妮·庞加莱见图1.2）。他们的祖父母总是有空陪他们散步、讲故事。叔叔阿姨和朋友们也常来探访，并经常住上几天，从不缺乏。这确实是一个充满活力的家庭。

庞加莱与洛努瓦家族

庞加莱家族在洛林根基深厚。家族中有议员 (parliament)、军人 (military)，以及律师 (lawyers)、药剂师、科学家 (scientists) 和其他专业人士 (professionals)。

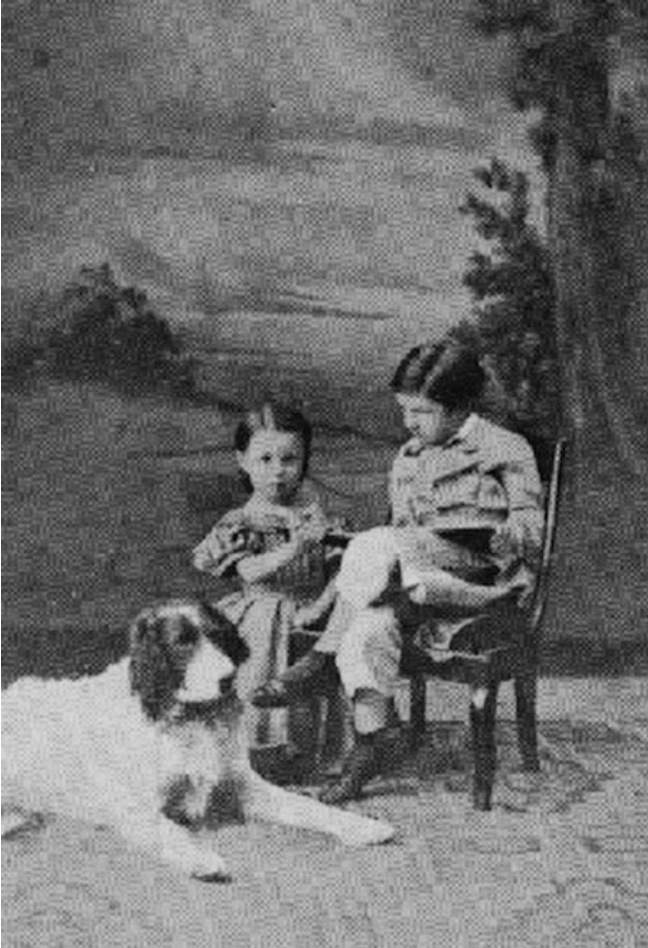图1.3 阿琳和亨利·庞加莱与狗汤姆

关于家族姓氏的起源存在不确定性：在古老的教堂和城镇记录中出现了诸如 Poinquarrez、Poingcarré 和 Pontcarré 等拼写。（根据他的导师及后来的同事加斯东·达布 (Gaston Darboux) 的说法，亨利更喜欢 Pontcarré 这个拼写。）

亨利的祖父雅克-尼古拉·庞加莱 (1794–1865)，于1813年在圣康坦 (Saint-Quentin) 开始了他的药剂师助手生涯，那一年拿破仑 (Napoleon) 在莱比锡 (Leipzig) 战败。1820年，他搬到南锡，并于1823年娶了锁匠的女儿凯瑟琳·罗兰 (Catherine Rollin)。如上所述，1833年他买下了马蒂尼公馆，在那里他将旧药房现代化，既用于制药也作为商店。他和妻子、孩子以及他的妹妹海伦 (Hélène) 住在这里；海伦总是穿着时髦优雅，与相当节俭的祖母凯瑟琳·庞加莱形成对比；亨利和阿琳称她为米内特姑妈 (Aunt Minette)。

雅克-尼古拉兴趣广泛。他给孙辈讲了许多家族故事，还教他们认识洛林的动植物。他的成就之一是编写了一本关于摩泽尔河谷 (Moselle valley) 植物群的书。

雅克-尼古拉和凯瑟琳有三个孩子：女儿克莱芒斯 (Clémence)，以及两个儿子安东尼 (Antoni) 和莱昂。克莱芒斯嫁给了一位药剂师，后来搬到了离南锡四公里的附近村庄埃耶库尔 (Heillecourt)。亨利和阿琳经常和母亲步行到这个村庄拜访他们好客的克莱芒斯姑妈。

安东尼·庞加莱 (1829–1911) 是巴黎综合理工学院 (École Polytechnique) 的优秀学生，学习土木工程 (civil engineering)。后来，他成为巴勒迪克 (Bar-le-Duc) 的国家道路桥梁总监。他写了几篇关于气象学 (meteorology) 的文章，并认识巴黎综合理工学院的一些教授，例如杰出的数学家拉盖尔 (Laguerre)。亨利在巴黎学习期间，安东尼叔叔经常去看他。一次探访后，亨利在给父母的信中写道：

安东尼叔叔今天早上离开了，满载着给巴勒迪克最重要人物的新年礼物。周三，我和他在塔隆 (Talon) 餐厅吃了晚饭，我们刚坐下，一位留着黑胡子的先生就走过来对他说：“啊，庞加莱先生，您好。”然后他立刻开始谈论摩泽尔地区的方言 (dialects) 以及巴勒迪克科学协会 (Scientific Society of Bar-le-Duc) 的各种活动。他离开后，安东尼叔叔告诉我，这个人是安德烈·图里埃 (André Theuriet)，曾在《两个世界评论》(Revue de Deux Mondes) 上发表文章 [Poincaré 2012]。

安东尼有两个儿子，雷蒙 (Raymond) 和吕西安 (Lucien)。雷蒙·庞加莱 (1860–1934) 在法国政治中扮演了重要角色，在第一次世界大战 (First World War) 期间及战后关键的头几年担任共和国总统 (president of the republic)（1913–1920）。他还多年担任财政部长 (minister of finance)、外交部长 (minister of foreign affairs) 和总理 (prime minister)。

吕西安·庞加莱 (1862–1920) 成为了法国中等教育总监 (directeur de l’enseignement secondaire)。

在一个政治名人声望远超科学家的世界里，南锡有一条大型商业街以雷蒙的名字命名，而一条更为普通的街道则以他的堂兄亨利的名字命名，这并不奇怪。比较一下《拉鲁斯插图百科全书》(Larousse Illustré) 中的条目也很有趣：雷蒙占了十六行，而亨利只分到了五行。

尽管庞加莱家族成员拥有重要的社会地位，但他们绝非循规蹈矩之辈。例如，安东尼尽管担任着显赫的总监公职，却在1852年政变 (coup d’état) 后拒绝向皇帝 (emperor) 宣誓效忠。

关于这种独立精神，家族中流传着一个关于亲戚加斯帕尔-约瑟夫·庞加莱 (Gaspard-Joseph Poincaré) (1762–1837) 的古老故事。他在巴黎学习，后来成为一名西多会 (Cistercian) 僧侣 (monk)。在修道院 (monastery) 里，他学习神学 (theology) 和数学，但最终因其非正统观点而被驱逐。离开修道院后，他仍然以牧师 (priest) 的身份活动，直到法国大革命 (French Revolution) 爆发。随后他被命令停止神职活动，但他拒绝服从并被监禁。他挺过了这次磨难，但后来放弃了圣职，组建了家庭，成为了一名受人尊敬的公民。

雅克-尼古拉希望儿子莱昂继承他的药房，但莱昂想去旅行，不希望从事一份将他束缚在柜台后的职业。雅克-尼古拉没有对儿子让步，但莱昂还是秘密地在斯特拉斯堡 (Strasbourg) 攻读医学课程，并成功完成了学业。直到考试结束后，他才告诉父亲自己的所作所为，并补充说他现在希望继续在巴黎深造。

雅克-尼古拉同意了儿子的请求，但始终将他的津贴维持在较低水平。莱昂·庞加莱成为了南锡备受尊敬的医生，在医学院 (medical school) 讲授解剖学 (anatomy) 和生理学 (physiology)。那时，大约在1860–1870年间，南锡存在一些高等教育机构，例如培养林业工程师 (forestry engineers) 的林业学校 (École Forestière)。还有广为人知的南锡学派 (École de Nancy)，提供建筑学 (architecture)、艺术 (art) 和工业设计 (industrial design) 的讲座。南锡学派在新艺术运动 (Art Nouveau movement) 中扮演了重要角色。

普法战争 (Franco-Prussian War) 后，阿尔萨斯 (Alsace) 的吞并使斯特拉斯堡大学 (University of Strasbourg) 划归德国 (German) 领土，因此该大学迁至南锡，南锡医学院与大学的医学系 (medical faculty) 合并。1878年，莱昂·庞加莱获得了医学系的教席 (chair)。

洛努瓦家族则代表了生活的另一面。亨利的外祖父母路易-欧仁 (Louis-Eugène) (1807–1874) 和欧芙拉西·马沙尔 (Euphrasie Marchal) (1806–1881)，被称为梅梅尔 (Mémère)，住在阿朗西的一片土地上，那里有一座大房子，部分是农场 (farm)，部分是大厅 (hall)；如今，这座房子被称为雷尼城堡 (Château Reny)。亨利和阿琳年幼时，假期通常在这里度过。从南锡到阿朗西的旅程，如今一两个小时即可完成，在当时却是一段相当长的旅途。乘火车 (train) 到达梅斯 (Metz) 后，会在那里的旅馆 (hotel) 住一晚，然后在早上乘坐邮政马车 (post coach) 前往布里埃-埃-皮埃尔蓬 (Briey-et-Pierrepont)，家里的马车 (carriage) 在那里等着将他们接到阿朗西。欧仁妮经常带着孩子们、她的妹妹奥迪尔 (Odile) 以及众多堂表兄弟姐妹、侄子侄女和其他家族成员待在那里。节日里，房子里可能会有多达六十位客人，他们吃饭、喝酒、散步、玩耍，外祖母洛努瓦（梅梅尔）是这一切的中心。（顺便提一句，外祖母在涉及数值计算 (numerical calculation) 和纸牌游戏 (games of cards) 的比赛中总是获胜。）

洛努瓦家族也出了不少科学家。例如，亨利的表兄阿尔班·阿莱 (Albin Haller) (1849–1925) 是一位杰出的化学家 (chemist)，也是法国科学院的成员。阿尔班娶了奥迪尔姑妈的女儿露西 (Lucie)，后来他和亨利成为了亲密的朋友。在去巴黎求学之前，亨利经常去阿朗西。

一场久病

1859年冬天，当时五岁的亨利生病了。他的父亲诊断他患有白喉 (diphtheria)，当时这是一种危及生命的疾病，没有可靠的治疗方法。亨利活了下来，但留下了无法行走或说话的后遗症。腿部的瘫痪 (paralysis) 很快就过去了，但说话很长一段时间都很困难。这段病程持续了九个月。

当急性传染 (contagion) 的危险过去后，三岁的阿琳可以再次探望亨利，但对他们俩来说，情况都非同寻常且困难。

他们找到了一种新的交流方式，亨利用手势 (gestured) 表达，阿琳学会了理解他。这使得他们的关系更加亲密。然而，这段生病的经历让亨利在身体上缺乏安全感。他行动笨拙，变得害羞，有点害怕参与粗野的游戏。小阿琳牵着他的手，引导他在房子里迈出了第一步。

对于一些孩子来说，长期患病后又经历一段瘫痪的创伤性经历 (traumatic experience)，可能会在他们一生中产生严重的影响。然而，就亨利而言，没有迹象表明存在这样的后遗症。那么，他是如何设法相对安然无恙地度过的呢？也许在这种卧病在床、无法说话的情况下，亨利的创造力 (creative faculties) 受到了激发。支持这种假设 (hypothesis) 的一个事实是，他通过手势与妹妹建立了联系。阿琳虽然只有三岁，但也起到了积极的作用。在他康复 (convalescence) 期间，亨利不耐烦和活跃的天性很快占据了主导。他想要坚持下去。简而言之，克服疾病后遗症的条件是有利的。

法国的初等和中等教育

在十九世纪，有初等教育 (enseignement primaire) 和中等教育 (enseignement secondaire) 的学校，但直到1880年代，并没有要求所有儿童都必须上学。对于那些上学的孩子，初等教育在十一岁结束，之后是在初级中学 (collège) 进行四年的中等教育。一个人可以通过在高级中学 (lycée) 再学习两到三年（至今仍然如此）来结束其中等教育。高级中学的期末考试通向业士学位 (baccalauréat)。通过这项考试的人就有资格接受高等教育 (higher education)。

1.2 学生时代：1860–1870

安东尼和莱昂·庞加莱兄弟对教育有很多共同的理念：教育应该范围广泛，同时内容充实。1860年，家族的朋友阿方斯·欣泽兰 (Alphonse Hinzelin) 向亨利的父亲提议，让男孩和他同龄的女儿一起接受私人辅导 (tutored privately)。（顺便说一句，欣泽兰是签署亨利出生证明的见证人之一。）一年后，埃米尔·欣泽兰 (Émile Hinzelin) 和阿琳也到了加入他们的年龄。

课程不是很系统，主要包括语法 (grammar) 和拼写 (spelling)、阅读练习、历史 (history) 和生物学 (biology)。带有植物群 (flora)、动物群 (fauna) 和地质特征 (geological features) 图片的书籍被用作补充教学。亨利的亲戚从未觉得他在做家庭作业 (homework)。他似乎能立刻将课程内容记在脑子里。

亨利的家人于1862年搬到了拉法耶特街 (Rue Lafayette) 6号，同年10月，八岁的亨利开始定期上学。这发生在他的姑妈奥迪尔和阿梅莉·洛努瓦 (Amélie Launois) 带着她们的儿子，即亨利的表兄弟路易 (Louis) 和罗杰 (Roger) 到达后不久。他们很快和亨利一起上学了，所有人都对新规则、噪音、不认识的学生和老师、新要求以及家庭作业的新奇事物感到兴奋。

亨利的班级由舒弗纳尔 (Chouvenal) 老师监管 [Bellivier 1956, p. 62]。开学第一周结束时，亨利在阅读方面名列班级第一，并在班级荣誉榜 (honours list) 上排名第一。这对他的私人教师欣泽兰先生来说并不意外。值得注意的是，法国的教育体系竞争非常激烈。学生们不断地被排名 (ranked)，这种做法对优秀学生是一种激励，但往往让天赋稍差的学生感到沮丧。这些排名列表至今仍然可用，因此很容易追踪亨利在学校的进步。

第一周的结果是整个学年的典型。在他班上的24名学生中，亨利在任何科目或任何作业上的表现从未低于第三名。他的私人教育显然相当不错，当然，事后看来，我们也知道亨利的才智过人。但更重要的是，从家庭的孤独和亲密到学校的压力和纪律 (discipline) 的相当快速的过渡进行得非常顺利。在接下来的几年里，亨利一直保持着班级前列的位置。

除了非凡的智力 (intelligence)，亨利还有非凡的记忆力 (memory)。他的论文导师及后来的同事加斯东·达布观察到 [Darboux 1913]，可能很少有人知道亨利·庞加莱年轻时懂得多少东西。他只需读一本书一遍就能完全掌握其内容；他能回忆起书中某个特定条目在哪一页、哪一行。在国外旅行多年后，他能背诵出火车停靠过的所有车站，以及他们住过的所有城镇和旅馆的名字。拥有这样的记忆力，他能在不做任何笔记的情况下掌握学校的课程也就不足为奇了。

1865年，十一岁的亨利和他的表兄弟路易、罗杰一起领受了第一次圣餐 (First Communion)，这是罗马天主教会 (Roman Catholic Church) 的圣事 (sacrament)，孩子第一次在祭坛 (altar) 上领受圣体 (Eucharist)，以神秘的方式象征基督 (Christ) 的身体。据他的妹妹阿琳说，亨利非常认真地对待这次活动 [Boutroux 1912]。

同年，1865年，亨利和阿琳进行了他们的第一次长途旅行，与父母一起前往法国东部的孚日山脉 (Vosges)，同行的还有哈代尔 (Xardel) 一家。哈代尔是莱昂·庞加莱在南锡医学院的同事；他家有五个孩子，其中包括一个名叫保罗 (Paul) 的男孩，与亨利同龄。达布 [Darboux 1913] 引用保罗·哈代尔的话说，在那次旅行中，两家人参观了以回声 (echo) 闻名的朗贝尔尚谷 (Vallée de Ramberchamp)。亨利向大家解释了回声的理论 (theory)，包括声速 (velocity of sound) 和距离 (distances) 所起的作用。注意到路边的电报电缆 (telegraph cables)，他滔滔不绝地讲述了电 (electricity) 在通过电报 (telegraph) 发送信息中的作用，一切都那么自然，毫无自负之意。

夏天，他们参观了科隆 (Cologne) 和法兰克福 (Frankfurt)，但假期的最后还是在熟悉的阿朗西度过。在这里，亨利根据圣女贞德 (Joan of Arc) 的生平创作了一部五幕剧 (play)，由他的妹妹、表兄弟路易和罗杰以及他自己表演。表兄弟之间发生了一场争吵，破坏了友好的气氛和一些舞台道具 (stage properties)。亨利提议将戏剧 (drama) 改编成歌剧 (opera)，演员们自己写咏叹调 (arias)，从而挽救了局面。这部歌剧在家族中大获成功。

1867年夏天，庞加莱一家，加上奥迪尔姑妈和表弟路易，参观了巴黎的世界博览会 (World Exposition)。除了展览品的奇观，孩子们还对餐馆 (restaurants) 服务速度之快感到惊讶。值得注意的是，孩子们被带去参加这类活动，因为在那个时代，通常是把孩子留在家里；有很多人可以照顾他们。然而，庞加莱和洛努瓦家族希望他们的孩子接受尽可能广泛和富有启发性的教育。两个家族都回到阿朗西，一起度过剩下的假期。受到巴黎印象的启发，亨利、阿琳和路易建立了一个政治实体 (political entity)，“特里纳西”(Trinasie)，一个由三个政府组成的联邦 (federation)。有宪法 (constitution)。亨利任命了各部部长，孩子们发明了三种语言以及一种共同语言，特里纳西语 (Trinasien)。这个联邦持续了几年，是许多事业的框架。

在1867–1868年期间，亨利将近十四岁时，他在中学的老师之一向他的母亲欧仁妮报告说：“亨利将成为一名数学家。”当她似乎不明白时，他补充道：“我的意思是一位伟大的数学家。”然而，亨利自己当时告诉阿琳 [Boutroux 1912]：“我不能对任何事做出承诺。我不知道二十年后我会做什么。”这对于那个年龄的男孩来说似乎是很自然的态度。在同一时期，亨利学习了舞蹈 (dancing) 和钢琴 (piano)。他成了一个不知疲倦的舞者，但钢琴方面并不成功。

接下来的一年，亨利十五岁时，进行了大量的戏剧表演 (theatrical performance)，但这次是面向更广泛的公众 (public)。亨利偏爱喜剧 (comedy)，据阿琳 [Boutroux 1912] 说，他发展出一种特殊的技巧：

亨利对表演有自己的想法。他会挑选观众中的一员，通常是一个易受感染、经常发笑且似乎欣赏表演的女孩。在这个观众和他自己之间建立了一种特殊的关系；当他不在舞台上时，她似乎会失落。他特别关注她，向她投去亲切的话语和会心的眨眼。结果是，他的表演显得非常滑稽，不仅对那个年轻女子如此，对全体观众也是如此。

这段经历表明亨利具有相当的社会意识 (social awareness) 和心理洞察力 (psychological insight)。他的剧团在南锡及邻近村庄演出，他们通常乘公共汽车 (bus) 前往，然后步行返回。

亨利的父亲莱昂从未放弃年轻时对旅行的热情。1869年，全家的年度旅行首先去了怀特岛 (Isle of Wight)，然后去了伦敦 (London)。想象一下他们的进取精神：父母带着13岁和15岁的孩子，他们中没有一个人会说英语 (English)，也没有人出过海。但这个家庭通过阅读狄更斯 (Dickens) 做好了准备。按照惯例，他们途经好客的阿朗西返回。他们几乎不知道，下次访问阿朗西时，他们心爱的社区将被战争摧毁。幸运的是，亨利祖父母的房子基本幸免。

南锡被占领

1870年7月19日，法国和普鲁士 (Prussia) 互相宣战，仅几周后，8月14日，普鲁士就占领了南锡。那年夏天没有颁发学校文凭。表弟路易被送上了去布鲁塞尔 (Brussels) 的最后一班火车，在那里继续学业。表弟罗杰加入了洛林的抵抗组织 (resistance)，如果被敌人抓获，将面临被即决处决 (summary execution) 的风险。庞加莱一家考虑离开城镇，但由于乡下的普遍混乱而放弃了这个想法。莱昂·庞加莱负责一辆救护车 (ambulance)，当时16岁的亨利担任医疗助理 (medical assistant)。

一位德国高级官员被安置在庞加莱家，亨利立即利用了这种情况。每天晚饭后，他会与那个人交谈以提高他的德语 (German) 水平，同时了解最新消息 [Boutroux 1912]。就这样，他为未来的旅行和学习做准备，同时努力获取尽可能多的关于当前局势的信息。在占领期间，消息主要来自德国报纸和其他德国来源。每天晚上，全家人都用字典 (dictionary) 翻译德国的战报。

1870年11月，经过一段极度不确定的时期后，从阿朗西传来了消息。消息不好，于是母亲欧仁妮带着亨利和阿琳出发去看望她的家人。旅途异常艰难。他们到处遇到士兵；梅斯在经历了数月的战斗后已成废墟；该地区普遍荒凉。到达后，欧仁妮发现她的父母情绪低落。他们最小的儿子，阿德里安 (Adrien)，一名军官 (army officer)，已被俘虏并押往普鲁士。阿朗西有传言说法国将军布尔巴基 (Bourbaki) 将解放南锡，但亨利摇了摇头：“那是不可能的” [Boutroux 1912]。他对布尔巴基的行动不抱太大希望。

对于法国人，尤其是阿尔萨斯和洛林的人民来说，这是一个极其困难的时期。政府 (government) 陷入混乱；法国军队 (French army) 似乎无能为力；法国大片地区被外国军队 (foreign troops) 占领。南锡人民目睹了破坏、亲人离散，甚至可能面临他们城镇并入德国这一几乎难以想象的命运。最终，南锡没有遭遇这样的命运，但这个噩梦在当时看来是完全可能的。阿尔萨斯变成了德国领土，梅斯镇也失去了。这些后果将在未来许多年毒害法德关系。

随后一年阿尔萨斯的吞并给南锡带来了许多逃亡者，其中包括一个十五岁的男孩，保罗·阿佩尔 (Paul Appell)，他成了亨利一生的朋友。

普法战争

十九世纪的欧洲见证了保守势力 (conservative forces) 在各地的复辟 (restoration)。1852年，第二共和国 (Second Republic) 垮台，被路易-拿破仑（拿破仑三世 (Napoleon III)）的波拿巴帝国政权 (imperial Bonapartist regime) 取代。德国仍然是独立公国的集合体，普鲁士在政治和军事上都是最强大的国家。普鲁士国王威廉一世 (Wilhelm I)（1861年至1888年在位）由他的“铁血宰相”奥托·冯·俾斯麦 (Otto von Bismarck) 辅佐治理国家。普鲁士推行积极的欧洲政策，这让法国人感到不安，尤其让拿破仑三世起了疑心。1870年，这种疑心促使法国向普鲁士宣战。在那个时代，人们仍然认为战争是“通过其他手段实现的政治” (politics by other means)，但在这种情况下，战争变成了一场灾难。

法国军队不是普鲁士军队的对手，很快巴黎就被围困。一个直接后果是拿破仑三世于1870年退位，随之而来的是君主制 (monarchy) 的终结。1871年，双方达成了和平协议，但法国国内的混乱是巨大的。经过保皇派 (monarchists) 和共和派 (republicans) 的长期斗争，法兰西第三共和国 (Third French Republic) 于1875年建立。另一个重要后果是普鲁士的实力和政治影响力得到承认，这使得俾斯麦得以推动建立统一的德国，各公国的君主承认普鲁士的威廉为他们的皇帝。

在和平谈判中，法国被迫将阿尔萨斯和洛林的大部分地区，包括梅斯但不包括南锡，割让给德国。法国人感到备受打击。这些领土的丧失将在1918年第一次世界大战后得以扭转。

1.3 中学与大学之间：1871–1873

为了被法国的精英学校（大学校 (grandes écoles)）之一录取，必须通过一项全国性考试，即入学竞赛 (concours)。为了准备考试，通常的做法是在高级中学 (lycée) 学习几年，在那里可以学习初级或更高级的课程（特殊讲座 (special lectures)），最终获得学士学位，即业士学位 (baccalauréat)。一些参加特殊讲座的学生会参加大学校入学竞赛。

要理解亨利·庞加莱的成长和发展，重要的是要注意到，他年轻时被认为是一个非常有天赋的孩子，但并非神童 (child prodigy)。他没有专攻某一学科，而是兴趣广泛，包括数学和物理、工程学 (engineering)、哲学 (philosophy)、艺术、表演，甚至舞台剧写作。他直系亲属和其他与这些不同兴趣相关的亲戚为他发展才能提供了理解、鼓励和保障。在这方面，人们可以将亨利与克里斯蒂安·惠更斯 (Christiaan Huygens) 相比较，后者在截然不同的时代和国家也拥有非常广泛的兴趣。惠更斯有具艺术天赋的兄弟，他的父亲是一位政治家 (statesman) 和著名的诗人 (poet) 及作曲家 (composer)。

在1870–1871年的普法战争期间，亨利开始在南锡高级中学准备文科 (arts) 业士学位。考试于1871年8月举行。亨利的总体成绩是“良好”(good)。除了拉丁文作文 (Latin composition) 外，他在各单项科目中的成绩都不突出。然而，他凭借一篇题为“一个国家如何才能提升自己？”(How can a country elevate itself?) 的哲学论文 (philosophical essay) 给人留下了深刻印象。这在当时的法国是一个非常切题的问题。

阿琳讲述 [Boutroux 1912]，亨利也准备参加理科 (sciences) 业士学位考试，但他的老师们不希望他同时参加两项考试，以免显得他准备不足就参加了考试。所以亨利在次年11月参加了考试，结果成了一场经典的考试噩梦。他考试迟到了一会儿，匆忙中误解了第一个涉及几何级数 (geometric series) 的问题。在他的答案中，他讨论了一个与题目不同的问题，这导致他在两个笔试部分的第一部分得了零分。他在另一道笔试题上的得分也不算出色，虽然他在四门口试问题上的得分还不错，但通常如果有一门得了零分是不能通过的。然而，考官们知道亨利是一位才华横溢的学生，所以他们让他以“尚可”(reasonably good) 的勉强资格通过了考试。每个问题的评分从零到五分。亨利的笔试成绩是0分和2分，口试成绩是3分、4分、2分、4分。

准备入学竞赛 (Concours)

亨利现在报名参加了为准备入学考试 (entrance examination)，即入学竞赛 (concours) 而设的特殊课程。在开始这些学习之前，他潜心研读了当时的数学教科书 (textbooks)。根据 [Bellivier 1956] 的记载，这些书包括鲁歇 (Rouché) 的《几何学》(La Géométrie)、贝特朗 (Bertrand) 的《代数学》(L’Algèbre)、迪阿梅尔 (Duhamel) 的《巴黎综合理工学院分析教程》(Cours d’Analyse de l’École Polytechnique) 以及沙勒 (Chasles) 的《高等几何学》(La Géométrie Supérieure)。列表上的后两本书尤其值得注意。让·迪阿梅尔 (Jean Duhamel) 的微积分 (calculus) 书是巴黎综合理工学院的教科书，迪阿梅尔 (1797–1872) 本人就在那里讲课。米歇尔·沙勒 (Michel Chasles) 的几何学 (geometry) 教材强调了分析 (analysis) 和几何学的互补作用；它具有原创性，难度大，受到一些同事的质疑，但文笔引人入胜。沙勒 (1793–1880) 在1846年索邦大学 (Sorbonne) 几何学教席的就职演讲中阐述了他的方法如下（亦见 [Chasles 1880]）：

如果人们知道几何学的主题是空间的度量 (measure) 和特性 (characteristics)，那么人们就知道这个领域有多么广阔，甚至不知道这个领域的边界在哪里。因为人们想象的空间会无限次地改变形状，而自然界中出现的或人类精神能够想象出的每种形式的特征本身就极其繁多，甚至可以说取之不尽。

但这本身就足够激动人心了，沙勒接着提议彻底改变几何学的实践方式。正如十九世纪初所理解和实践的那样，例如在约瑟夫-路易·拉格朗日 (Joseph-Louis Lagrange) 的影响下，古典几何学 (classical geometry) 变得非常分析化；简而言之，它现在强调公式 (formulas) 而非图形 (pictures)，强调分析而非综合 (synthesis)。拉格朗日本人在他的《分析力学》(Mécanique Analytique) 的引言中写道：

在这部著作中找不到图形。我在此阐述的方法既不需要几何或力学的构造或论证，只需要由规则和统一的步骤强制执行的代数运算 (algebraic operations)。

沙勒则这样说：

人们可以看到分析和几何各自的优势：前者凭借其变换的神奇机制，迅速地从起点通向终点，但往往不揭示所走的路径或所用众多公式的意义。另一方面，几何学从对事物的深思熟虑和思想的有序安排中汲取灵感。它必须以自然的方式发现那些分析可能忽略和忽视的陈述。

当沙勒的《高等几何学》于1852年问世时，他关于几何学的观点，当然是以分析作为支撑，是相当革命性的。它很可能对亨利的思维方式产生了重要影响，特别是考虑到分析与几何的富有成效的结合，这是他方法的典型特征，例如在他后来发展的动力系统的定量 (quantitative) 和定性 (qualitative) 理论中。这一推测在 [Poincaré 1905b, 第5章, p. 153] 中得到支持，庞加莱在该处谈到拉普拉斯方程 (Laplace equation) 所唤起的分析和几何意象时写道：

借助这些意象，人们可以一目了然地看到纯粹演绎 (pure deduction) 需要经过连续步骤才能展示的东西。

在1871–1872学年期间，他的一位老师说服亨利也参加林业学校 (L’École Forestière) 的入学考试。他在林业学校考试中获得第二名，而在第一学年结束时，他自己学校（高级中学）的总考 (general examination) 中获得第一名。事后看来，从今天的角度看，建议亨利参加林业学校考试似乎很奇怪，但必须认识到南锡的林业学校是一所著名的工程学院。它成立于1824年，提供多样化的课程 (curriculum)，当然也包括数学。它招收了许多外国学生 (foreign students)。数学家埃米尔-埃马纽埃尔·勒尼奥 (Émile-Emmanuel Regneault) (1834–1866)，一位活跃的研究者，是该校的教员之一。

然而，1872年最激动人心的事件几乎是偶然发生的。那年夏初，巴黎综合理工学院入学竞赛的数学题公布了。答案要晚些时候才会公布。在此期间，亨利的母亲注意到儿子总是在房子里踱来踱去。事实上，他正在尝试解决这个问题。而且他成功了！这一壮举传到了家族之外。保罗·阿佩尔于1872年9月开始在高级中学上特殊课程，他讲述道：

在学年的最初几天，一个同学指着亨利·庞加莱对我说：“这是个聪明的家伙。他在林业学校考了第二名，在总考的初等数学 (elementary mathematics) 中得了第一名，而且他独自解出了巴黎综合理工学院今年的考题。”庞加莱的外表给我留下了深刻印象；乍一看，他似乎不是通常那种聪明的学生。他似乎沉浸在自己的思绪中；他的眼睛仿佛被思想蒙上了一层纱。当他说话时，他的眼睛透露出他的善良天性；那是一双既闪烁又深邃的眼睛。我被他吸引了，由于我们都是走读生 (day students)，我们在放学时交谈了几句。他说话的方式给我留下了深刻印象，断断续续，中间有长时间的沉默 [Appell 1925a]。

他的表达方式对他实现抱负构成了潜在障碍。阿佩尔指出：

从你第一次在课堂上听到他讲话，他高水平的才智就显而易见。当他回答问题时，他省略了所有的中间推理过程，而且他的话语非常简洁，以至于老师总是要求他澄清答案，并补充说：“如果你在考试中这样回答，你可能会冒着不被理解的风险” [Appell 1925a]。

提出这一意见的数学老师是维克多·埃利奥 (Victor Elliot) (1847–1894)。

和大多数特殊班级的老师一样，他是自己领域的专家 (expert)。他曾在巴黎高等师范学院 (École Normale Supérieure) 学习，并将于1876年在皮瑟 (Puiseux)、埃尔米特 (Hermite) 和布里奥 (Briot) 的指导下进行博士论文答辩，他们都是杰出的数学家。在他职业生涯的后期，他担任了贝桑松大学 (University of Besançon) 的系主任。

不仅是亨利的简洁让人们起初感到恼火。埃利奥老师和其他同学注意到亨利不怎么写字。他总是只有一张纸，偶尔在上面做些笔记。不仅如此，几天后，他们发现那总是同一张纸。他真的是一个认真的学生吗？事实证明确实如此。他知道自己在做什么，而且总是乐于帮助同学。他们的恼火很快变成了钦佩和友谊。

亨利和保罗·阿佩尔的相遇是一生友谊的开始。阿佩尔描述道 [Appell 1925a]，放学后，他们和另一个朋友哈特曼 (Hartmann)——像保罗一样来自阿尔萨斯——常常一起长途散步，三个朋友谈论数学问题，也谈论哲学问题、战争、德国占领以及法国的政治未来。皇帝已经退位，他们都支持建立第三共和国。据阿佩尔说，高级中学里几乎所有的学生都支持共和国。

亨利和保罗当时都期望着未来在巴黎综合理工学院学习。然而，他们的老师埃利奥建议他们也申请巴黎高等师范学院，结果是他们不得不在1873年夏天准备两场入学考试。

法国精英学校 (Les Grandes Écoles de France)

法国的大学校 (grandes écoles) 代表了一种在法国普通大学体系 (university system) 之外的高等教育类型。它们的建立是为了基于才能 (merit) 向更广泛阶层的学生开放高等教育。拥有合适类型的业士学位，就可以进入大学。而对于大学校，则必须参加入学考试，为此要在高级中学 (lycée) 的特殊班级进行准备；在报读这种特殊班级之前，可以先获得文科或理科的业士学位。

大学校大约成立于1800年，法国许多最伟大的政治和学术界杰出人物都毕业于这些学校。在亨利时代，它们包括：

巴黎高等师范学院 (École Normale Supérieure)，由蒙日 (Monge) 和卡诺 (Carnot) 创立。
巴黎综合理工学院 (École Polytechnique)，一个具有军事性质 (military character) 的机构，由一位将军 (general) 担任校长。学生穿着制服 (uniforms)，毕业后通常成为正规军官 (regular officers) 或预备役军官 (reservists)。
矿业学院 (École des Mines)，一个培养矿业工程师 (mining engineers) 的机构，侧重于科学和工程。
圣西尔军事专科学校 (École Spéciale Militaire de Saint-Cyr)，为正规陆军军官 (regular army officers) 提供标准教育。

这四个机构的讲师都是杰出的数学家、科学家和工程师。如今，有更多的大学校，例如巴黎高等师范学院在巴黎以外设立的分校，以及强调政府管理、管理学 (management) 和经济学 (economics) 的新机构。

大学校录取：入学竞赛 (Concours)

1873年，亨利·庞加莱和保罗·阿佩尔是南锡特殊班级中仅有的两名参加大学校考试的候选人 (candidates)。巴黎高等师范学院的入学考试 (concours) 于7月在巴黎举行，达布是考官之一。正如他以前的考试一样，亨利的过程并不顺利。考试题目是两个二次曲面 (quadrics) 的投影 (projection) 和交线 (intersection)，亨利没有采用显而易见的经典方法。此外，他在画图时犯了一个错误。口试后，一位考官得出结论，他表达得不好。亨利排名第五，而保罗排名第三。

几个月后，这个结果在巴黎高等师范学院引起了讨论。通过保罗的斡旋，副校长贝尔坦-莫罗 (Bertin-Morot) 甚至安排了一次与亨利的会面，讨论这次不幸的考试结果。但那时改变事件的进程已经太晚了。

巴黎综合理工学院的笔试于1873年8月4日至6日在南锡举行。亨利很紧张，考试结束后对自己的表现表示失望。考题是几何题，表述如下：

给定一个二次曲面 $S$ 和其上的两个点 $A$ 和 $B$ 。存在无限多个二次曲面 $R$ ，它们在 $A$ 点和 $B$ 点与 $S$ 相切 (tangent)。求：

曲面 $R$ 中心的轨迹 (locus)；
这些曲面与平行于给定平面的切平面 (tangent planes) 的接触点 (contact points) 的轨迹；
同一些曲面与经过给定直线的切平面的接触点的轨迹。

离开考场时，他们发现世界变了样。整个南锡都洋溢着兴奋；每个旗杆上都挂着旗帜，到处都是庆祝的人群。就在那天，德国军队撤离了这座城市。保罗的心情复杂，因为他的家乡阿尔萨斯仍将是德国领土的一部分。

巴黎综合理工学院入学委员会的数学家有布里奥、布凯 (Bouquet) 和皮瑟。至于结果，则无需担心，因为实际上，亨利的考试成绩非常好。后来，在巴黎的口试中，他给考官们留下了深刻的印象。来自南锡的熟人德罗什·迪·泰卢瓦 (De Roche du Teilloy) 当时在场 [Bellivier 1956]。他回忆说，亨利被要求给出一个初等几何 (elementary geometry) 的证明 (proof)。他毫不犹豫地给出了一个正确的答案，但考官接着要求一个更初等的证明。亨利对此的即时回答也是正确的，但包含了三角学 (trigonometric) 的论证。考官现在要求一个只包含初等几何论证的证明，并再次立即得到了令他完全满意的回答。考官们非常高兴。亨利在巴黎综合理工学院的考试中获得第一名，他将在那里继续他的学业。保罗则进入了巴黎高等师范学院。未来，在巴黎不同的学校里，他们将不得不更加努力才能见面。日常接触的时期结束了，至少在几年内是这样。

阿琳知道哥哥很快就要搬出家门了。这个前景让她脸色苍白、日渐消瘦，以至于在1873年夏天，她的父亲带着全家去海边住了几周；像往常一样，假期的最后一部分是在阿朗西度过的，尽管那里已遭破坏。但这仍然是阿琳的一段艰难时期。

第二章大学教育：1873–1879

1873年秋，当时19岁的亨利 (Henri) 在母亲和妹妹的陪伴下前往巴黎 (Paris)，入读巴黎综合理工学院 (École Polytechnique)。在巴黎期间，亨利的母亲和阿琳 (Aline) 住在林克 (Rinck) 家，他们是来自洛林 (Lorraine) 的老朋友，其子埃利·林克 (Élie Rinck) 与亨利同龄。她们在巴黎待了一周，期间探望了亨利，并第一次看到他穿军装 (uniform) 的样子（见图2.1）；她们觉得告别非常困难。这种感觉是相互的，证明这一点的是，在巴黎的头两年里，亨利给家里写了数百封信，平均每周超过两封。

2.1 艰难的一年

正如我们将看到的，军校 (military school) 的生活并不轻松。1873年，有两百多名新生（确实都是男性；女性不被录取），他们都必须上课、进行军事训练 (military drill)、学习使用武器、站岗，并轮流值勤。在相对较少的空闲夜晚，亨利会去好客的林克家或他的亲戚奥莱里 (Olleris) 家，或者去看戏。在社交方面，他与同学的关系或多或少和在南锡 (Nancy) 时一样。他过于沉浸在自己的思想中，没有积极的社交生活。休息时，他常常独自散步，但在必要时会提供帮助，并且因其知识和洞察力而受到尊重。他听课时总是双臂交叉，常常不做笔记。有时，他会突然参与社交活动，这一点也被同学们接受。我们稍后会讨论其中的一些场合。阿佩尔 [Appell 1925a] 描述了亨利和一位同学之间典型的问题讨论：

如果有人问他问题，他会亲密地挽着对方的胳膊，迫使对方和他一起走，但方式很不规则。他会突然向前冲，然后骤然停下，接着又向后走。这有点类似于物理学家所说的布朗运动 (Brownian motion)。

图2.1 穿着巴黎综合理工学院军装、表情略显 bewildered (困惑) 的亨利·庞加莱

亨利觉得有些讲座很有趣，特别是埃尔米特 (Hermite) 的分析学 (analysis) 课。那一年，他的其他教授包括雷萨尔 (Résal)（力学 (mechanics)）、曼海姆 (Mannheim)（几何学 (geometry)）、法耶 (Faye)（天文学 (astronomy)）、科尔尼 (Cornu)（物理学 (physics)）、弗雷米 (Frémy)（化学 (chemistry)）和泽勒 (Zeller)（历史学 (history) 和文学 (literature)）。课外，学生们的学习由博内 (Bonnet) 和其他讲师，包括阿尔芬 (Halphen) 指导。皮埃尔-奥西安·博内 (Pierre-Ossian Bonnet) (1819–1892)，见图2.2，阐述并证明了微分几何 (differential geometry) 中的一些重要结果。高斯-博内定理 (Gauss–Bonnet theorem) 使用了几何曲率 (geometric curvature) 的概念，是他成就的一个著名例子（高斯 (Gauss) 通过一个例子阐述了该定理；博内提供了通用定理）。乔治·亨利·阿尔芬 (George Henri Halphen) (1844–1889) 在1870–1871年的普法战争期间担任法国军队军官，并因此获得勋章。他的数学家生涯始于战后。他的研究涉及微分方程 (differential equations) 的不变量 (invariants) 和微分几何。他44岁时去世。

在给家里的信中，亨利很少提及自己的学术成就。下面这封信的片段是个例外：

一天埃尔米特生病了；接替他的拉盖尔 (Laguerre) 在课上讨论了一个特定问题。因为黑板 (blackboard) 上的字迹不清，我没有做笔记。我没太在意，但几天后，一个同学问我是否能给他解释一下这个问题。我回答说我没做笔记，但我会重构拉盖尔的证明。我这样做了，或者说我认为我这样做了，但同时，我感到有些不确定，因为在我记下的唯一备注在证明中没用上。那天晚上，这位学生被叫去参加初步考试 (preliminary examination)，阿尔芬正好问他这个问题。学生展示了我的证明。考官问这是否是他自己的证明。学生找到我，问是不是我的，然后回去告诉阿尔芬。阿尔芬说他一点也不惊讶。阿尔芬告诉了拉盖尔，拉盖尔派人找我，告诉我我的证明比他的更简单。这个证明将取代他的证明，出现在那些我认为被冠以《巴黎综合理工学院档案》(Archives of the École Polytechnique) 这样浮夸名称的出版物中。

图2.2 皮埃尔-奥西安·博内，亨利·庞加莱就读期间巴黎综合理工学院的教务长

1873年初，学生排名如下：1. 庞加莱，2. 博纳富瓦 (Bonnefoy)，3. 佩蒂迪迪埃 (Petitdidier)。这三位学生在班级中一直保持最高排名，直到期末考试。然而，到了春天，亨利的情绪变差，从第一名掉了下来。他觉得教学水平太低，并且怀念难题带来的挑战。1874年5月，他沮丧地写道：

这里就像一个巨大的机器，你必须跟上它的运转，否则就会被碾压；人们做着我们之前二十代综合工科学校学生做过的事情，以及我们之后 $2 n + 1$ 代新生将要做的事情。

这里只需要智力的两个方面：记忆力 (memory) 和口才 (eloquence)。要理解一门课程，你只需要下功夫，这就是为什么任何人如果真的想通过死记硬背 (grinding away) 超过我，都可以做到。考官从不问任何激动人心的问题。

他并非总是如此沮丧，恰恰相反，但他始终将自己在巴黎综合理工学院的两年视为通往未来的必要阶段，而不是本身有趣的经历。如果他去了巴黎高等师范学院 (École Normale) 会不会更好？也许吧。当他去巴黎高等师范学院拜访朋友保罗·阿佩尔时，他经常遇到该校的一些讲师。例如，他曾与数学家布里奥 (Briot) 共进晚餐。那些会面给了他很大的乐趣。巴黎综合理工学院不乏才华横溢、富有启发性的讲师，如埃尔米特、拉盖尔和阿尔芬。然而，在一个旨在培养军官和工程师的教学环境中，他们并不十分突出。

尽管如此，亨利第一年的创造力并未被扼杀。1874年10月，他的第一篇研究论文发表了，主题当然是几何学：“De´monstration nouvelle des proprie´te´s de l’indicatrice d’une surface”（曲面指示曲线性质的新证明）发表在《数学年刊》(Annales de Mathématiques)，第二辑，第十三卷。这是一篇关于曲率 (curvature) 和密切曲面 (osculating surfaces) 的有趣习作。一个学生能独立撰写并发表这样的论文，无疑应该给人留下深刻印象，但几何学教授对此有何看法呢？这将在后面间接揭晓。

我们先来看一件发生在1874年初的事件。每次上课，都会指定一名学生总结前一堂课的内容。准备工作是集体努力，最优秀的学生会帮忙。有一天，学生们的准备工作进展不顺，他们向亨利求助。他说：“别找了；题目错了。”由于他们的总结是官方布置的任务，学生们告知了教务长奥西安·博内。相关讲师曼海姆教授被要求解释。曼海姆坚持认为题目表述是正确的，但很久以后，与那次讲座相关的问题从课程 (curriculum) 中被移除了。

在亨利第一学年末，几何学考试由儒勒·德·拉古尔纳里 (Jules de la Gournerie)（被称为古尔纳尔 (Gournard)）负责监督，他是曼海姆的朋友。亨利在几何学上得分很低，总成绩排在第二，仅次于博纳富瓦，但领先于佩蒂迪迪埃。很明显，古尔纳尔因为亨利绘图 (drawings) 的质量而严厉地扣了他的分：绘图一直是的弱项。整个学校都为这种不公正而骚动。林克夫人在亨利学生时代总是热情接待他，她想提出正式投诉，但亨利劝阻了她。重要的是，像校长博内这样的重要人物也同感普遍的愤慨，这就足够了。

终于，1874年的暑假开始了。正如阿琳所说：“我们过得像是在参加一场永恒的派对。我们做了亨利喜欢的一切事情，一切让他高兴的事情” [Boutroux 1912]。

2.2 在巴黎综合理工学院的第二年

第二学年开局良好，亨利的第一篇科学论文得以发表，但亨利的心情并非总是愉快的。他苦于缺乏智力刺激，并觉得争取班级第一名并不适合他。争取班级第一不仅仅是为了在同学中争优；在法国，获得学校排名的第一名是开启职业生涯下一步的关键。然而，亨利的兴趣远在这些琐碎的学校事务之外。幸运的是，他与同学们相处得很好，此外，第二年，他得以迎接一些来自南锡的老同学来到巴黎综合理工学院，其中包括哈特曼 (Hartmann)，这也对他有所帮助。他与排名上最主要的竞争对手博纳富瓦相处融洽。

他继续给家里写很多信，包括单独写给阿琳的信，但信写得越来越潦草，包含的关于他在巴黎日常生活的信息也越来越少。有几次他因病住进综合工科学校的医务室几天，但病情都不严重。最糟糕的是，他最喜欢的科目——几何学，掌握在曼海姆和古尔纳尔手中。

1875年，第二学年末的考试来临。亨利在地形学 (topography)、绘图和建筑学 (architecture) 上失分。班级排名变为：1. 博纳富瓦，2. 庞加莱，3. 佩蒂迪迪埃。

才华横溢的学生博纳富瓦和佩蒂迪迪埃后来都因矿难英年早逝。亨利与曼海姆的矛盾还有后续——或者更确切地说，可以算是一种清算。1886年拉盖尔去世后，次年选举法国科学院 (Académie des Sciences) 的新成员。庞加莱和曼海姆都在提名名单上。32岁的庞加莱以34票当选，而回顾其漫长而富有成效的几何学生涯的曼海姆获得了24票。

2.3 矿业学院 (L’École des Mines)

1875年11月，当时21岁的亨利与他在巴黎综合理工学院的同学博纳富瓦和佩蒂迪迪埃一起，继续在巴黎的矿业学院 (École des Mines) 接受高等教育。今天，在二十一世纪，教育可能性几乎无限，这个选择似乎相当不太可能。但在1875年，选择并不多。矿业学院当时（现在也是）一所优秀的工程学院 (engineering school)，为一种有用且具有重要社会意义的职业——矿业工程师 (mining engineer) 提供教育。亨利的另一种可能性是进入巴黎大学（索邦大学 (Sorbonne)），但这会给他提供更通识的教育，而不是直接使他具备从事某种职业的资格。亨利将成功完成矿业学校的学业，但他的兴趣只在少数几个课题上，特别是矿物学 (mineralogy)。他毫不费力地保持着最优秀学生之一的地位，但他对排名失去了兴趣。

成为一名矿业工程师

在矿业学院的第一年，亨利的课程包括矿山管理 (mine management) 和机械 (machinery)、冶金学 (metallurgy)、矿物学、地质学 (geology)、古生物学 (palaeontology)、化验 (assaying)、绘图和英语 (English)。

院长多布雷 (Daubrée) 是亨利的远亲，他坚持认为亨利在矿业学院期间不应该关注数学。12月，亨利写信回家：

今天早上我去见了多布雷先生。他非常和蔼，并像安东尼叔叔一样告诉我，他建议我在完成学业之前不要搞数学。看来博内曾请求允许我免修某些课时，以便我可以去索邦大学听课。他告诉我他拒绝了。我回答他说我完全理解。

关键在于亨利不需要索邦大学的讲座来准备他们的数学考试。博内给他提供练习题，1876年8月，他通过了索邦大学的数学考试。

在第一年期间，他定期去巴黎综合理工学院拜访博内。因此在1876年初，亨利写道：“周三我又去拜访了博内，他非常和蔼。我还见到了布凯 (Bouquet)，他尽可能地和蔼。他借给我一本我需要的旧书。”

在矿业学院学习，同时在索邦大学学习，并没有干扰亨利的社交生活。他继续给家里写信，尽管频率比在巴黎的头两年稍慢。信中描述了看戏、拜访亲戚以及政治问题，并常常包含幽默的诗句。经历了普法战争和阿尔萨斯被吞并的经历后，南锡对德国的军事实力，特别是洛林（包括南锡）可能被吞并的问题，仍然存在相当大的忧虑。亨利写信告诉家人，在他看来，这种事态发展极不可能，因为它需要对充满敌意的洛林法国居民进行永久的军事占领。他补充道：

更可能的是普鲁士吞并比利时 (Belgium) 和荷兰 (Holland)。这对我们来说将非常不幸，因为它会使我们与德国的边界长度增加一倍，并使德国海军 (navy) 力量加倍；它将为德国提供富饶的殖民地 (colonies)，更不用说荷兰的工业财富以及由此给我们带来的极其不利的军事态势。

亨利接着暗示，在比利时和荷兰之后，波西米亚 (Bohemia) 和德国东部的国家将是下一个目标。大约六十年后，亨利的所有担忧都变成了现实。

时不时地，埃米尔·布特鲁 (Émile Boutroux) 的名字会出现在家信中。1876年，布特鲁被任命到南锡大学讲授哲学。他成了庞加莱家的常客。埃米尔·布特鲁于1878年10月与阿琳结婚。

这位年轻的哲学家对笔迹学 (graphology) 感兴趣，这导致他经常与亨利的堂兄雷蒙·庞加莱 (Raymond Poincaré)（当时在南锡学习哲学）以及在巴黎的亨利进行讨论。1877年秋，雷蒙搬到巴黎学习法律 (law)。他在圣米歇尔大道 (Boulevard St. Michel) 租了亨利隔壁的房间。表兄弟之间原本远距离进行的哲学讨论现在变得更加密集了。

如上所述，笔迹学，即研究性格与笔迹之间关系，引起了亨利的兴趣。在一封家信中，他表示惊讶，根据他的经验，女性常常思维随意、缺乏逻辑 (logic)，但她们的笔迹却常常整洁有序。这让他反思自己的书写：

就我而言，我发现我的主要特征可以在我的笔迹中辨认出来。我把每个单词的最后一个字母写得很小的方式说明我没有耐心等待。我的柔韧性体现在圆润笔画的柔和中，只有最初的影响才能加以修正。看看我的n和u，它们看起来像希腊字母 $ω$ ，而不像你们那样像德文字母w。另一方面，看看我的字行排列得像刚从村子里出来的车辆（与巴鲁瓦（Barrois）线条的普鲁士式协调性相比，真是天壤之别）。正是这个特点暴露了我完全缺乏在法国人民中如此普遍的官僚主义情绪 (bureaucratic feelings)。

图2.3 亨利·庞加莱论地球运动

（巴鲁瓦，指雷蒙·庞加莱。）关于亨利笔迹的样本，例如，参见图2.3所示的页面。

图2.4 堂兄雷蒙·庞加莱 (1860–1934) 作为一位主要政治家的形象。他后来成为总理和共和国总统

雷蒙·庞加莱 (1860–1934)

雷蒙·庞加莱，见图2.4，是亨利叔叔安东尼的儿子之一。他出生在巴勒迪克，在巴黎大学学习法律。作为一名律师，他后来在儒勒·凡尔纳 (Jules Verne) 的诽谤诉讼 (libel suit) 中为其辩护。他于1893年，33岁时成为政府部长，并在五个政府任期内担任总理 (prime minister)。雷蒙在1913–1920年的关键时期担任共和国总统 (president of the republic)，这一时期涵盖了第一次世界大战 (First World War) 和战后条约谈判（凡尔赛条约 (Treaty of Versailles)）。在与德国的关系以及索取战争赔款 (war reparations) 问题上，他持强硬立场。

他的弟弟吕西安·庞加莱 (1862–1920) 是一位物理学家，后来成为公共教育总监 (inspector-general of public instruction)。雷蒙和亨利即使在后来的职业生涯中也一直保持联系，例如讨论任命和为杰出人士颁发奖章等事宜。他们两人都是享有盛誉的法兰西学术院 (Académie Française) 的成员。

完成矿业学院的学业

矿业学院为其学生组织为期数天的短途考察，但通常在学习期间会有两次在国外的较长停留。1877年夏天，第二学年末，亨利与同学勒科尔尼 (Lecornu) 一起前往奥地利 (Austria) 和匈牙利 (Hungary)。那次旅行后，他写了两份报告，一份是关于匈牙利的煤矿，另一份是关于白镴工业。勒科尔尼后来写信告诉朋友们，亨利在旅途中是多么快乐，以及他收到并阅读阿琳写给他的长信时是多么高兴 [Appell 1925a]。

类似的教学考察在第三学年末，即1878年进行，这次是和博纳富瓦一起。他们前往瑞典 (Sweden) 和挪威 (Norway)，这次旅行后，亨利又写了两份关于采矿作业的报告。

1878年6月，亨利在矿业学院的学习结束了。最终排名亨利第三，仅次于博纳富瓦和佩蒂迪迪埃，但这个结果似乎并未引起他的兴趣。次年，1879年3月，24岁的亨利·庞加莱被任命为沃苏勒 (Vesoul) 的矿业工程师职位，该地离南锡相对较近。这项任命由国家矿业监察局 (National Inspection of Mines) 作出，任命措辞为“任命为三级普通矿业工程师，负责沃苏勒矿物学分区 (mineralogical subdistrict) 并兼管东部铁路 (railways) 的监督工作”。正如我们将看到的，这份工作并非没有危险。博纳富瓦和佩蒂迪迪埃也成为了矿业工程师。他们在二十多岁时因在执行任务过程中发生的事故而去世。

亨利在沃苏勒的活动是短暂的。1879年12月，他被任命为诺曼底 (Normandy) 卡昂 (Caen) 理学院 (Faculté des Sciences) 的数学讲师。形式上，他一生都是矿业工程师团 (corps of mining engineers) 的成员。1910年6月16日，他被任命为矿业总监 (inspector-general of mines)，在这种情况下，这很可能是一个荣誉头衔。

2.4 数学学位论文

在这些年的所有活动中，亨利的数学讨论和研究从未中断。似乎亨利几乎是在矿业学院的第二和第三年期间，不经意间写完了他的学位论文 (dissertation)；数学细节参见第9.1节。其灵感来自布里奥和布凯在《巴黎综合理工学院杂志》(Journal de l'École Polytechnique) [Briot and Bouquet 1856] 上发表的一篇关于微分方程解的论文。作为初步成果，亨利写了一篇短文，并提交给了同一份杂志 [Poincaré 1878]。这篇题为《由偏微分方程定义的函数的性质》(Les proprie´te´s des functions de´finies par des e´quations aux de´rive´es partielles) [Poincaré 1916, Vol. 1] 的学位论文，于1877-1878年之交提交给了他的导师达布 (Darboux)、拉盖尔和博内。亨利费了些周折才得到他们的评语。1878年他写道：

达布住在36号与好表妹同住一屋。他的建议我欣然接受不久之后收到长篇大论洋洋洒洒十大页；去拉盖尔处运气不佳，本想请教，可惜啊，大门紧闭，怒火中烧，奔向奥西安，也是木门一扇。但我终会找到他，感谢上帝。

图2.5 庞加莱诗意不满的原文（南锡庞加莱档案馆提供）

“好表妹”是他亲戚奥莱里 (Olleris) 家的女儿。法文原文复制于图2.5；文本如下：

Or donc Darboux logeait nume´ro 36 Dans la meˆme maison que la bonne cousine. Avec un grand plaisir je rec¸us ses avis et peu de temps apre`s une longue tartine. Remplit dix grand pages; Moins heureux chez Laguerre ou` dirigeant mes pas Je voulais recueillir des conseils, mais he´las, Je trouvais porte close et, le coeur plein de rage, Je cours chez Ossian, porte de bois aussi. Mais je le trouverai quelque jour, Dieu merci.

学位论文在一年半后的1879年8月1日被接受。它写得很匆忙，导师们提出了许多批评意见。很久以后，加斯东·达布这样描述他作为导师的角色 [Poincaré 1916, Vol. 2]：

约瑟夫·贝特朗 (Joseph Bertrand) 曾说，布里奥和布凯阐述其结果的那篇文章，是自欧拉 (Euler) 以来在分析学这一领域取得的最大进展。亨利·庞加莱通过研究和完善这项伟大工作首次亮相。在他于1878年提交的学位论文中，他投身于一个更困难的问题，即具有任意数量自变量 (independent variables) 的偏微分方程 (partial differential equations) 的积分。乍一看，我就清楚地认识到，这份手稿超出了常规水平，包含了足够写好几篇优秀论文的材料。但为了准确地描绘庞加莱的工作方式，我们必须不回避地指出，其中有许多地方需要修正或解释。庞加莱凭直觉思维 (intuitive thinking)……对他来说，进行我认为必要的修正和清理是很容易的。但他后来向我解释说，在我要求他这样做的时候，他正忙于完全不同的概念。无论如何，他的学位论文因其包含的若干新的重要思想而具有价值。

庞加莱后来与达布谈话时提到的新思想，很大一部分包含在他的革命性回忆录 [Poincaré 1881] 以及他关于二次型 (quadratic forms)、三次型 (cubic forms) 及其不变量和所谓的福克斯函数 (Fuchsian functions) 的文章中，这些文章发表于1880年和1881年（以及更晚）；参见 [Poincaré 1916]。福克斯函数，或称自守函数 (automorphic functions)，将在下一章和第八章讨论。该回忆录在第9.2节讨论。它提出了一种全新的方法来研究非线性二阶微分方程 (nonlinear second-order differential equations) 的理论。它给出了奇点 (singular points) 的分类、闭曲线 (closed curves) 的指标定理 (index theorem)、“后继点”(consequents) 或平面系统 (plane systems) 的庞加莱映射 (Poincaré map) 的思想，以及关于极限环 (limit cycles) 的庞加莱-本迪克松定理 (Poincaré–Bendixson theorem) 的基本思想。它现在已成为常微分方程 (ordinary differential equations) 一般理论的一部分，庞加莱在接下来的几年里就这个主题发表了大量著述。因此，这篇学位论文不能与关于平面微分方程全局定性与定量分析 (global qualitative and quantitative analysis) 的回忆录 [Poincaré 1881] 分开来看。

在学位论文本身中，处理是局部分析 (local analysis) 的，用可能包含弱奇点 (weak singularities) 的特征方程 (characteristic equations) 来分析一阶偏微分方程 (first-order partial differential equations)。这导致了技术上复杂的分析，涉及许多不同的情况。可以理解，导师们需要时间来消化这些材料，并且他们要求提供例子来说明理论。不幸的是，论文中提供的例子不多。论文中极具价值的是庞加莱引入的新概念。我们提到代数体函数 (algebroid functions)、今天称为庞加莱域 (Poincaré domain) 的概念，以及特征值 (eigenvalues) 共振 (resonance) 的概念。后两个思想将在庞加莱关于动力系统 (dynamical systems) 的工作中经常出现，例如在太阳系 (solar system) 方程中，更普遍地出现在使用范式 (normal forms) 的一般近似方法 (approximation methods) 中，即所谓的庞加莱-杜拉克范式 (Poincaré–Dulac normalization)。

第三章在沃苏勒和卡昂取得的惊人成果

在考察包括科学家和艺术家在内的创造性人物的生活时，人们经常观察到，在最初的知识和实践技能积累期之后，会有一个活动爆发期，期间偶有中断。对亨利·庞加莱 (Henri Poincaré) 来说，这个分水岭大约出现在1878年。然而，就他而言，重要成果的巨大洪流在他一生中从未中断。

3.1 在沃苏勒担任矿业工程师

从1878年夏天到1879年12月，对亨利来说是一段忙碌而不平静的时期。他必须完成在矿业学院 (École des Mines) 的学业，完成并答辩他的数学学位论文，同时还要找一份工作。1879年3月28日，他毕业成为一名矿业工程师 (mining engineer)，并被任命为法国东部沃苏勒 (Vesoul) 的矿业监察员 (inspector of mines)。他曾请求一个离南锡 (Nancy) 不太远的职位。

他于1879年4月3日抵达沃苏勒，时年将近25岁，主要负责距离沃苏勒约30公里的龙尚 (Ronchamp) 矿区。作为一名矿业工程师，庞加莱的工作是评估矿山的生产能力和安全性，包括结构完整性、通风 (ventilation) 以及易燃气体的定位和清除。

最初几个月，下矿井和写报告的工作是例行公事。然而，在1879年9月1日清晨，新开的马尼矿 (Magny mine)（见图3.1）发生了一起爆炸。当班的22名矿工中，有16人在650米深处因爆炸丧生。在救援行动进行期间，亨利·庞加莱下到矿井开始调查。在一份详尽的报告中，他描述了矿井的通风和巷道系统 (gallery system)，并指出爆炸的一个可能原因是发现了一盏穿孔的安全灯 (safety lamp)（从煤层 (coal seam) 中采煤所需的光线由安全灯提供；当时当然没有电）。

图3.1 位于沃苏勒附近龙尚的马尼矿，1879年曾发生爆炸。亨利·庞加莱曾下到该矿井并提交了一份报告。

他作为沃苏勒监察员的最后一份报告是关于马尼矿的新通风系统，是他与同事特劳特曼 (Trautmann) 共同撰写的。报告于1879年11月30日签署并提交（见图3.2），一天后他就在卡昂 (Caen) 担任了数学讲师的新职位。他继续在矿业工程师组织——矿业工程师团 (Corps des Mines) 中担任职务。1893年，他晋升为总工程师 (chief engineer)，如上所述，1910年，他成为法国矿业总监 (inspector-general)。

在沃苏勒，亨利将时间分配给矿业工程师的工作和数学研究。他在这两方面都具备资格，并且同时从事这两种职业。在那段时期，他的堂兄雷蒙·庞加莱 (Raymond Poincaré) 写了两部小说。在沃苏勒，亨利也写了一部小说，是一个从未出版的浪漫故事。手稿已经丢失，但故事情节梗概可以在 [Bellivier 1956] 中找到。

3.2 在卡昂担任讲师

1879年12月1日，亨利·庞加莱被任命为卡昂大学 (University of Caen) 的数学分析 (mathematical analysis) 讲师，见图3.3。大约在同一时间，保罗·阿佩尔 (Paul Appell) 在第戎 (Dijon) 获得了一个大学职位，埃米尔·皮卡 (Émile Picard) 则在图卢兹 (Toulouse) 任职。根据达布 (Darboux) [Darboux 1913] 的说法，法国大学当局努力将高素质的科学家任命到外省的大学，而不是让他们全部集中在首都。这当然是个好主意，但两年后，这三人又在巴黎重聚了。

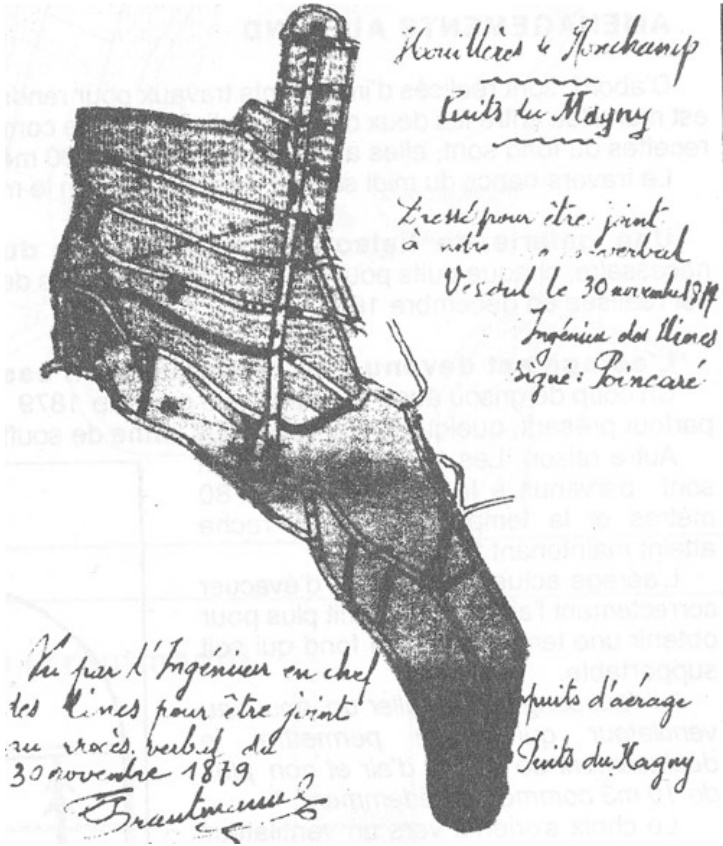图3.2 为龙尚马尼矿设计新通风系统的报告首页，由庞加莱和特劳特曼签署（龙尚矿业博物馆 (Musée de Mines, Ronchamp) 提供）

对亨利来说，那是一个充满变化的时期，首先是在一个新城市担任新职位，现在有时间更深入地思考新的数学问题。观察到亲戚（包括他的妹妹阿琳 (Aline)）和朋友们结婚，也激发了他自己寻找伴侣的兴趣。大约在1880年，亨利结识了路易丝·普兰·当德西 (Louise Poulain d’Andecy)。他们于1881年4月20日结婚，几个月后他被任命到巴黎索邦大学 (Sorbonne) 任职。

在卡昂，他与昔日的同学和旅伴勒科尔尼 (Lecornu) 重逢，后者是当地的矿业工程师。勒科尔尼回忆 [Bellivier 1956] 他们是如何度过1879年新年前夜的。亨利似乎比平时更加心事重重：

我记得我邀请他在1879年12月31日和我的父母一起过来吃晚饭。他整个晚上都在踱来踱去，不听别人说话，只用寥寥数语回答。他完全忘记了时间，以至于我决定友好地提醒他现在已经是1880年了。那一刻，他似乎清醒过来，决定告辞。

图3.3 庞加莱在卡昂（诺曼底 Normandy）开始了他的大学生涯。卡昂大学成立于1432年，当时位于圣索沃尔 (Saint-Sauveur) 区。这些建筑以及大部分老城在1944年7月7日的盟军轰炸中被摧毁。

考虑到庞加莱将在他的回忆录 [Poincaré 1881] 以及稍后关于福克斯函数 (Fuchsian functions) 的文章中发表的一系列激动人心的思想，这种心不在焉是可以理解的。在他的回忆录中，庞加莱发展了我们今天所知的常微分方程的定性理论 (qualitative theory)，即奇点——现在通常称为临界点 (critical points)——的分类和命名：结点 (node)、焦点 (focus)、鞍点 (saddle) 和中心点 (centre point)；横截线 (transversal) 到自身的映射（庞加莱映射 (Poincaré map)）的概念；以及极限环 (limit cycle) 的概念，后者后来被表述为庞加莱-本迪克松理论 (Poincaré–Bendixson theory)。[Poincaré 1881] 中的处理还详细说明了可能的极限环数量以及对某些困难情况的分析。这篇回忆录开启了常微分方程领域一个全新的研究方向。

3.3 自守函数 (Automorphic Functions)：与富克斯和克莱因的联系

庞加莱对微分方程及其应用的兴趣引导他沿着与代数 (algebra) 和复分析 (complex analysis) 紧密相关的方向发展数学。富克斯 (Fuchs) 的一篇文章激发了他给作者写信。稍后，他与费利克斯·克莱因 (Felix Klein) 进行了广泛的通信。他关于自守函数 (automorphic functions) 的大部分论文都发表在这些年（1881–1884），但庞加莱对这个主题一直保持着兴趣。他在1907年发表了一篇关于单值化 (uniformization) 的重要论文。事实上，他关于自守函数的出版物几乎填满了他的全集中的整整一卷。这些论文的英译本以及引言可以在 [Poincaré 1985] 中找到。

图3.4 拉扎鲁斯·伊曼纽尔·富克斯 (Lazarus Immanuel Fuchs) (1833–1902) 曾在柏林 (Berlin)、格赖夫斯瓦尔德 (Greifswald)、哥廷根 (Göttingen) 和海德堡 (Heidelberg) 任教。他对具有奇点 (singularities) 的线性微分方程感兴趣。

在本节中，我们将描述庞加莱与富克斯和克莱因的联系。自守函数的一些更技术性的方面在第八章描述。

3.3.1 与富克斯的联系，1880–1881

德国数学家拉扎鲁斯·伊曼纽尔·富克斯 (1833–1902)，见图3.4，在柏林师从库默尔 (Kummer) 和魏尔斯特拉斯 (Weierstrass)。他曾在柏林、格赖夫斯瓦尔德、哥廷根和海德堡任职，1875年至1884年在海德堡讲学。1884年，他回到柏林，接替库默尔在柏林大学 (University of Berlin) 的职位。与庞加莱的联系发生在富克斯在海德堡期间。富克斯对线性常微分方程 (linear ordinary differential equation, ODE)

\frac{d^{2} y}{d z^{2}} + P (z) \frac{d y}{d z} + Q (z) y = 0,

的复值解 (complex-valued solutions) 的特性感兴趣，其中 $P (z)$ 和 $Q (z)$ 是复变量 (complex variable) z 的有理函数 (rational functions)。函数 $P (z)$ 和 $Q (z)$ 在复平面 (complex plane) $ℂ$ 的孤立点处有极点 (poles)（奇点）；其策略是寻找解在极点邻域内的局部级数展开 (local series expansions)。众所周知，所谓的指标方程 (index equation) 在此过程中发挥作用。富克斯从两个独立解 $f (z)$ 和 $g (z)$ 开始，定义商 $f (z) / g (z) = η (z)$ ，并在 [Fuchs 1880] 中断言 $η (z)$ 的反函数

是一个亚纯函数 (meromorphic function)（亚纯意味着除了若干孤立点处有极点外处处解析 (analytic)）。富克斯关于该主题的第一篇论文 [Fuchs 1880] 的处理并不完整；例如，他排除了对数项 (logarithmic terms) 的存在。

早些时候，富克斯曾与埃尔米特 (Hermite) 就具有奇点的微分方程进行过通信。1878年，法国科学院 (Académie des Sciences) 为以下问题的最佳处理方案设立了一个奖项：“显著改进单自变量线性微分方程的理论。”这个问题是由查尔斯·埃尔米特 (Charles Hermite) 提出的，他熟悉富克斯工作所引发的问题；提交作品的截止日期是1880年的最后一天。埃尔米特作为评审团的重要成员，负责评估参赛作品。这样的奖项竞赛是十八和十九世纪由欧洲各学术团体和贵族赞助的一系列科学竞赛之一。通常会宣布一个奖项竞赛，设立评审团，并规定提交截止日期。为确保匿名性，参赛作品需装在密封信封中提交，并附带一句短语或句子以便日后识别作者。奖项竞赛将众多科学家的注意力集中在一个重大的科学问题上。通过这种方式，它们在激励研究方面发挥了重要作用。

1880年3月，庞加莱向科学院提交了他的文章，随后他又提交了修订版和若干补充。在 [Gray and Walters 1997] 中可以找到对这些贡献的详尽描述。该奖项最终授予了阿尔芬 (Halphen)；庞加莱获得了荣誉提名奖 (honourable mention)。大约在同一时间，1880年5月29日，庞加莱写信给富克斯：

我怀着极大的兴趣阅读了您发表在最新一期《克雷尔杂志》(Journal de Crelle) 上的题为“关于反演问题推广”(U¨ ber die Verallgemeinerung des Kehrungsproblems) 的卓越论文。尊敬的先生，我希望您能允许我就此主题向您请教一些澄清。[此处省略了关于可能假设的讨论。]

然而，人们本可以提出一千种其他的假设。尊敬的先生，我必须承认，这些想法让我对您所发表结果的普适性产生了一些疑问，因此我冒昧地就此事与您联系，希望澄清此事不会给您带来麻烦。

事实上，庞加莱在这封信中证明了富克斯只讨论了他问题的一个特例。随后是一系列的信件往来，可以在 [Poincaré 2012] 以及 [Poincaré 1916, Vol. 11] 中找到。庞加莱用法文书写，富克斯用德文回复，但这似乎并未造成任何沟通困难。在他于1880年6月5日从海德堡发出的第一封信中，富克斯甚至为用德文书写而致歉，并提到他确信庞加莱阅读德文没有问题，而德文是他能够最清晰表达自己的语言。富克斯尽管比庞加莱年长21岁，但始终保持着友好和感兴趣的口吻，即使在他开始清楚地认识到他年轻的法国通信者正在发展一种与他自己截然不同且更完整的方法时也是如此。1880年6月12日，庞加莱从卡昂写信给富克斯：

我发现在只有两个奇点的情况下，您引入的函数具有非常显著的特性，并且因为我打算发表我获得的结果，我请求您的允许称它们为福克斯函数 (Fuchsian functions)；因为是您发现了它们。

后来，这种“福克斯”的命名在庞加莱和费利克斯·克莱因之间引起了困难。与此同时，庞加莱分析了许多其他情况，发现了与各种特殊函数 (special functions) 的联系，例如椭圆函数 (elliptic functions)、超几何函数 (hypergeometric functions) 和 zeta 福克斯函数 (zeta Fuchsian functions)。

1908年，在他生命的晚期，庞加莱在一篇题为“数学的发明”(The Invention of Mathematics) 的随笔中回顾了这些发现。他回忆说，当他在卡昂工作时，他参加了诺曼底矿业学院组织的一次地质考察 (geological excursion)：

旅途中的事件使我忘记了我的数学工作。当我们到达库唐斯 (Coutances) 时，我们上了一辆公共马车 (omnibus)，准备带我们去开始散步的地方，就在我踏上台阶的那一刻，一个想法突然出现在我的脑海中，尽管我之前的思绪似乎并未为此做任何准备，那就是我用来定义福克斯函数的变换与非欧几里得几何 (non-Euclidean geometry) 的变换是相同的。我无法验证它，我没有时间这样做，我继续我正在进行的谈话，但我立刻感到了绝对的确定性。当我回到卡昂后，为了让自己安心，我不慌不忙地验证了我一直记在心里的结果。

库唐斯的公共马车如图3.5所示。1881年3月20日，庞加莱从卡昂给富克斯写了最后一封信，总结了他的成果：

我继续研究以您命名的函数，并希望很快发表我的结果。这些函数包含椭圆函数以及模函数 (modular function) 作为特例。利用这些函数以及我称之为 zeta 福克斯函数的其他函数，可以解决：

所有只有三个奇点（两个有限，一个无限）的有理系数 (rational coefficients) 线性微分方程。
所有有理系数的二阶方程。
大量具有有理系数的各阶方程。

至此，启发了庞加莱的富克斯的原始文章已经淡出视线。庞加莱正在创建一个全新的数学领域，即自守函数，它很快吸引了对一般复函数理论感兴趣的数学家们的注意：来自黎曼 (Riemann) 学派的数学家们。

3.3.2 与克莱因的通信：1881–1882

1881年中期开始了一场广泛的信件交流，总共26封，对象是费利克斯·克莱因 (1849–1925) [Poincaré 2012], [Poincaré 1916, Vol. 11]。在其职业生涯中，克莱因（见图3.6）曾在多所大学任职，始于埃尔兰根 (Erlangen)。在他与庞加莱通信期间，他在莱比锡 (Leipzig) 讲授几何学（1880–1886）；从1886年起，他在哥廷根担任教席。克莱因主要感兴趣的不是微分方程本身，而是利用这类方程来定义那些使复函数保持不变的变换。最简单的类型之一是周期函数 (periodic functions)，其变换是自变量按周期平移。以周期函数 $\exp (2 π i z)$ 为例。该函数在平移群 (group of translations) $z \mapsto z + n$ ， $n \in ℤ$ 下保持不变。离散 (discrete) 和连续变换 (continuous transformations) 在克莱因和庞加莱进行的微分方程分析中扮演着重要角色。保守微分方程 (conservative differential equations) 发挥着突出的作用，这类方程描述能量守恒的物理系统。这类保守方程通常包含整族的周期函数。观察在描述这些函数时数学思维和力学思维的混合是很有趣的。在此背景下，庞加莱在他为1880年科学院奖项竞赛提交的论文的第一份补充材料中写道，该材料重印于 [Gray and Walters 1997, p. 35]，并提到了罗巴切夫斯基 (Lobachevsky) 的欧几里得几何 (Euclidean geometry) 和非欧几里得几何：

图3.5 十九世纪末库唐斯（诺曼底）的马拉公共马车，从火车站开往市中心。

那么，什么是几何学？它是研究由图形在不改变其形状的情况下进行位移所形成的一群运算 (group of operations)。在欧几里得几何中，这个群由旋转 (rotations) 和平移 (translations) 组成。在罗巴切夫斯基的伪几何学 (pseudo-geometry) 中，它要复杂得多。

图3.6 费利克斯·克莱因

克莱因于1881年6月12日写给庞加莱的第一封信中，告知他已阅读了庞加莱关于福克斯函数的部分论文。克莱因接着描述了他所获得的成果类型，并解释了一些基本方面。1881年6月15日，庞加莱从卡昂礼貌地回复道：

您的来信表明，在福克斯函数理论方面，您比我更早地获得了一些结果。对此我毫不惊讶，因为我知道您对非欧几里得几何非常了解，而这正是我们所关心问题的真正关键……当我发表我的结果时，我会在这方面给予您应有的评价。

庞加莱接着提出了一些问题，并就克莱因对模函数术语的使用发表了评论。克莱因于6月19日立即作答，清楚地表明了困扰他的问题所在：

我反对“福克斯函数”这个称谓，尽管我完全理解您是通过富克斯的工作得到这些想法的……我不否认富克斯先生在微分方程理论其他分支的巨大功绩，但恰恰在这个领域，他的工作有许多不足之处；因为唯一一次他在给埃尔米特的信中解释模椭圆函数时，他犯了一个根本性的错误，后来被戴德金 (Dedekind) 过于宽容地评论了。

克莱因还列举了黎曼学派中与他合作研究离散和连续变换群理论的众多数学家及其各自的贡献。庞加莱给克莱因的信给人的印象是，他对黎曼学派的工作并不知情，但他写道他很可能能够重构那些思想。在他1881年6月22日给克莱因的回信中，他写道：

关于福克斯函数的名称，我不会改变。我对富克斯先生的尊敬禁止我这样做。除此之外，确实，这位海德堡数学家的观点与您和我的观点完全不同。同样确定的是，他的工作是我在这方面理论研究的起点和基础。

克莱因于6月25日相当傲慢地回复道：

如果你对整个文献都了如指掌，你对 F. 的看法就会不同。

在信中，克莱因的口吻更像是导师而非同事，但庞加莱似乎并不介意。他很珍惜这次对话，也许是因为他身边没有可以讨论此类话题的同事。关于富克斯，庞加莱在1881年6月27日回复道：

关于富克斯先生和福克斯函数的名称，很明显，如果我知道施瓦茨 (Schwarz) 的工作，我会选择另一个名称。但我是在发表我的结果之后，才从您的信中了解到这一点的，所以我不能再更改名称而不失对富克斯先生的尊重。

他补充了一些关于克莱因寄给他的论文的问题和评论。日期为7月2日、5日和9日（1881年）的第7、8、9封信包含了广泛的数学讨论，其中黎曼的复分析越来越多地发挥作用。与此同时，庞加莱已经采取行动，以克莱因的名字命名了某个函数类。关于此事，克莱因于7月9日从莱比锡写道（第9封信）：

您给这个函数类附加的名称让我有些惊讶，因为我所做的不过是指出了这个群的存在。就我而言，我既不会使用“福克斯”也不会使用“克莱因”的标示，而是坚持我的“包含线性变换的函数”。

事实证明，在当今数学界，人们在这方面遵循了克莱因的做法，只有在极少数地方还能找到用“福克斯”一词来指代自守函数。然而，“福克斯群”(Fuchsian groups)——这个术语也是由庞加莱创造的——作为在模形式 (modular forms) 理论中很重要的一类群的名称得以保留。下一封信来自1881年12月，同样来自克莱因。他进入了人生的一个困难时期。他患有哮喘 (asthma) 和抑郁症 (depression)。他从《科学院报告》(Comptes Rendus) 杂志上看到了庞加莱最新成果的根本性新颖之处，以及它们接踵而至的速度。1881年12月4日，克莱因寄出了一封包含提议的信：

在祝贺您取得深远成果的同时，我想提出一个能满足您我双方利益的建议。我想请您为《数学年刊》(Mathematische Annalen) 撰写一篇或长或短的论文，或者如果您抽不出时间完成这样的工作，可以给我寄一封信，在信中阐述您观点和结果的主要思路。然后我会在信后附上一份注释，解释我对整个领域的看法……当然，在付印之前，我会将这份注释给您过目并征得您的同意。

克莱因之所以能提出这样的建议，是因为他是《数学年刊》的主编。

1881年10月19日，亨利·庞加莱被任命为索邦大学的讲师 (Maître de Conférences)。他于12月8日从巴黎盖-吕萨克街 (Rue Gay-Lussac) 66号回信给克莱因，表示他将撰写克莱因建议的论文。克莱因于12月10日热情地回复，建议庞加莱的文章占据《数学年刊》16页的篇幅，并请他尽快提交文章，以便所有内容能在1882年3月发表。他没有解释为何如此匆忙。庞加莱很可能认为这只是神经紧张所致。

早在1881年12月17日，庞加莱就提交了他承诺的综述论文，并且确实在1882年初发表了 [Poincaré 1882]。克莱因于1882年1月13日感谢他的贡献，并将他要附加在论文后的注释寄给了庞加莱。同时，他告知庞加莱他将撰写一篇自己的短文，包含一些进行中的结果。然而，克莱因注释的语气比他之前信件中的评论更加强硬。摘录几句：

施瓦茨先生和我很久以前在所讨论领域发表的研究涉及的是福克斯函数，而富克斯先生对此并未发表任何东西。

在一系列类似的评论之后，我们看到了真正的地盘划分，将庞加莱的工作也纳入其中：

也许借此机会在这些小评论中补充一点是正确的，即这里讨论的所有研究，无论是几何推理还是与线性微分方程解相关的更具分析性的工作，都基于黎曼的思想。这种连贯性甚至更大，因为可以说，在庞加莱先生的研究中，真正重要的是黎曼在其学位论文中提出的广义复函数纲领的进一步延续。

庞加莱对此作何反应？他写了一封短信（系列中的第15封），评论说他无意改动克莱因注释中的任何内容，但他希望在自己的文章中增加几行，以便更好地证明“福克斯”这一名称的合理性。他稍后在1882年3月28日和30日的信件中这样做了。

这场讨论恰逢克莱因的困难时期，或者说他的困难与同庞加莱的交流之间可能存在联系。在回顾复函数理论的发展时 [Klein 1924]，转载于 [Poincaré 1916, Vol. 11, pp. 27–28]，克莱因叙述说他在1881–1882年期间生病了，遵医嘱于1882年3月去了德国北海 (North Sea) 沿岸的海滨度假地诺德奈 (Norderney)。由于天气不好，他只待了八天，但尽管时间短暂且哮喘发作，他还是提出了一个重要的定理，他称之为“中心定理”(Zentraltheorem)。途经杜塞尔多夫 (Düsseldorf) 返回时，他在几天内写下了该定理及其证明，然后寄往《数学年刊》发表。手稿的副本寄给了施瓦茨、胡尔维茨 (Hurwitz) 和庞加莱。每个研究者都体会过理解并解决一个难题、将其清晰表述并寄出发表时的那种兴奋感。然而，克莱因的证明并不完整。施瓦茨（见图3.7）和庞加莱都表示怀疑并指出了其中的漏洞；起初，施瓦茨甚至不相信该定理是真的。想象一下，当庞加莱在1882年4月4日写信时，克莱因该有多恼火：

图3.7 赫尔曼·施瓦茨 (Hermann Schwarz)，魏尔斯特拉斯的学生

非常感谢您上次寄给我的注释。您提到的结果确实让我感兴趣，我告诉您原因。我在一段时间前就已经发现了它们，但没有发表，因为我想把证明再弄清楚一些。这就是为什么当您那边澄清之后，我想知道您的证明。

这是惊人的坦诚，是亨利·庞加莱的典型风格，但克莱因在他的回忆录中写道，转载于 [Poincaré 1916, Vol. 11, pp. 27–28]：

他是如何以及何时知道的，他从未告知我。可以理解，这在我们的关系中造成了一定的紧张。

庞加莱是否意识到这次交流对克莱因的重要性是值得怀疑的。后者处于不利地位，就像任何一个在他不知情的情况下，庞加莱同时也在研究同一个问题的人一样。两人没有就克莱因定理的证明进行进一步讨论。

现在回到《数学年刊》以及庞加莱对克莱因附加注释的反应。庞加莱在3月28日写道，他不希望《数学年刊》的读者认为他冤枉了某人。他在3月30日寄给克莱因的补充说明（第17封信）中，详细辩护了他决定以富克斯和克莱因的名字命名函数的理由，同时赞扬了施瓦茨和黎曼的工作与成就。

克莱因于1882年4月3日怒气冲冲地回复，通知庞加莱他将在《年刊》中插入庞加莱的补充说明，并附上一篇后记再次重申自己的观点。他最后评论说，就他而言，关于函数命名的争论已经结束，并表示希望两人能就共同感兴趣的问题保持定期联系。

庞加莱于4月4日立即作答。他以讽刺的口吻开头：

您声称为了科学，您希望结束一场毫无结果的辩论，对此我只能祝贺您的决定。我知道这对您来说不会付出太大代价，因为如您所知，在附加于我最后文字的注释中，您将拥有最后的话语权。尽管如此，我还是为此感谢您。

在就富克斯的功绩以及与数学问题相关的疑问发表了一系列评论后，他总结如下：

我希望我们因一个名字而起的争执，这次是以礼貌的方式进行的，不会改变我们良好的关系。无论如何，我并不怨恨您首先发起攻击；我希望您也不会因为我为自己辩护而见怪。顺便说一句，延长关于一个名字的讨论是荒谬的，“名字不过是声音和烟雾”(Name ist Schall und Rauch)，说到底，我不在乎。您想怎么做就怎么做；至于我，我也会做我想做的事。

引用的“名字不过是声音和烟雾”出自歌德 (Goethe) 的《浮士德》(Faust)，克莱因是否对此感到高兴，至少是值得怀疑的。对他来说，姓名和声誉，以及对自己和亲密同事发现的优先权的恰当承认，至关重要。后续还有六封信，包含了详细的数学讨论，语气友好。庞加莱于1882年9月22日的信是最后一封，此后，两位研究者之间的通信停止了，尽管他们两人都将在未来许多年里继续研究自守函数。例如，1906年，庞加莱向《数学学报》(Acta Mathematica) 的编辑米塔-列夫勒 (Mittag-Leffler) 提交了一篇关于解析函数单值化的论文 [Poincaré 1999, 信件 232]。

这场争吵是否情绪过激了？经常周游欧洲并担任许多数学家信任代表的米塔-列夫勒写信给庞加莱 [Poincaré 1999, 信件 17]，说他拜访了施瓦茨，后者对庞加莱选择的名字“怒不可遏”(beside himself with fury)。幸运的是，当施瓦茨于1884年4月访问巴黎时，庞加莱和施瓦茨之间的关系有所改善 [Poincaré 1999, 信件 29]。人们可以主张采取理性的态度，即争吵可以通过双方说“让我们求同存异”(Let us agree to disagree) 来解决，但这否认了无法否认的情感和抱负。当时，施瓦茨渴望获得柏林大学的教授职位。对克莱因来说，名字的选择显然非常重要，但可能还有另一个因素在起作用。我们所描述的通信发生在一个莱比锡的资深教授和一个来自卡昂的初出茅庐的年轻数学家之间。后者结果是一位数学神童，一个总是在同一课题上遥遥领先于其他所有人的天才。当克莱因和他的学生们研究具体问题时，庞加莱从一开始就以极大的普适性阐述了理论；亦参见 [Freudenthal 1954] 中的评论。

费利克斯·克莱因是一位杰出的数学家，名誉和声望对他来说至关重要。当他研究庞加莱也感兴趣的课题时，他的运气不佳。与庞加莱的对抗必定在情感上对他造成了代价，但值得注意的是，尽管在函数命名上存在诸多不和谐，这两位伟大数学家之间的通信实际上是多么的礼貌和文明。

第四章在巴黎的职业生涯

亨利·庞加莱 (Henri Poincaré) 和路易丝·普兰·当德西 (Louise Poulain d’Andecy) 的婚礼于1881年4月20日在巴黎 (Paris) 举行。他们在巴黎的第一个家位于盖-吕萨克街 (Rue Gay-Lussac) 66号。后来，他们搬到了克洛德·贝尔纳街 (Rue Claude Bernard) 63号。1887年，他们的第一个孩子，女儿让娜 (Jeanne) 出生；几年后又生了两个女儿，1889年的伊冯娜 (Yvonne) 和1891年的亨丽埃特 (Henriette)。1893年，他们的第四个也是最后一个孩子，儿子莱昂 (Léon) 出生。

庞加莱档案馆 [Poincaré 2012] 中只有五封日期为1886年和1887年、亨利写给路易丝 (Louise) 的信（见图4.1），没有路易丝写给亨利的信。这些信非常亲切，例如开头是：“我最亲爱的宝贝，我收到了你的信。我崇拜你。”结尾是：“我最亲爱的宝贝，我非常非常爱你”[Poincaré 2012, Louise 0ab]。信中记述了与各种人物的会面、旅馆房间的质量以及有趣的八卦。庞加莱喜欢旅行，路易丝偶尔会陪伴他。她在一个著名的知识分子家庭长大，了解这种环境的特殊要求，她为亨利和他们的孩子提供了一个幸福安稳的家。他们一起参观展览、听音乐会。庞加莱尤其喜爱交响乐 (symphonic music)。

在庞加莱家族，就像所有家庭一样，有生也有死。在亨利和路易丝的第三和第四个孩子出生之间的那一年，亨利的父亲莱昂·庞加莱于1892年5月21日去世。因此，他活到看见了他的三个孙女，但没能见到他的孙子。

亨利的母亲欧仁妮 (Eugénie) 五年后于1897年7月15日去世。亨利因此事备受打击，此后几个月里，他不回复任何信件，将自己封闭在家庭中。在那年7月31日写给瑞典数学家约斯塔·米塔-列夫勒 (Gösta Mittag-Leffler) 的一张便条 [Poincaré 1999, 信件 143] 中，他写道自己无法工作，也不能讨论任何审稿或编辑论文的请求。8月3日，米塔-列夫勒回信表示理解和同情。直到10月11日，庞加莱才恢复了他的通信。

1897年8月，第一届国际数学家大会 (First International Congress of Mathematicians) 在苏黎世 (Zurich) 召开。庞加莱是组委会成员，并被邀请致开幕词。事实上，在他母亲去世前，他已经提交了演讲稿。庞加莱觉得无法出席，瑞士同事热罗姆·弗拉内尔 (Jérôme Franel) 代他宣读了题为“关于纯粹分析与数学物理的关系”(Sur les rapports de l’analyse pure et de la physique mathématique) 的演讲（论纯粹分析 (pure analysis) 与数学物理 (mathematical physics) 之间存在的相互关系）。大会大约有35场全体报告 (plenary lectures)，其中一场由费利克斯·克莱因 (Felix Klein) 主讲。庞加莱开幕词的文本收录在哲学著作 [Poincaré 1905b] 中；本书在第6.5节讨论了这篇演讲。

图4.1 亨利·庞加莱和路易丝·普兰·当德西在1881年结婚时的照片

庞加莱于1881年10月19日被任命为巴黎索邦大学 (Sorbonne) 理学院 (Faculté des Sciences) 的讲师 (maître de conférences)。这类职位是最近才设立的；其想法是在正式教授 (regular chair) 席位旁配备一位类似辅导员 (tutor) 或指导员 (coach) 的角色，一位合格的讲师，负责照看他的学生，给他们布置问题和练习，并批改他们的论文。除了这些任务，这位讲师可以进行自己独立的研究。

直到31年后他于1912年去世，庞加莱一直居住在巴黎并在此工作，在许多领域展现出非凡的创造力 (creativity) 和生产力 (productivity)。本章我们将鸟瞰他的活动。一些方面将在单独的章节和小节中得到特别关注，而更具技术性的方面将在本书的第二部分处理。

4.1 科研生涯概览

在获得索邦大学讲师职位后，庞加莱很快又获得了其他任命。1883年11月6日，庞加莱获得了在他以前就读的学校——巴黎综合理工学院 (École Polytechnique) 担任辅导员的额外职位；他一直担任此职直到1897年3月1日。

虽然这个辅导员职位有助于建立专业联系，但1885年3月16日被任命为索邦大学物理与实验力学 (physical and experimental mechanics) 教授席位则提供了更多的可能性。庞加莱当时30岁。然而，这项任务的实验方面远不如理论方面适合他，但很方便的是，另一个教席很快空缺出来。1886年夏天，他接替加布里埃尔·李普曼 (Gabriel Lippmann) (1845–1921) 担任数学物理与概率论 (mathematical physics and probability) 教席；李普曼转向实验物理学 (experimental physics)，并因其在照相工艺 (photographic processes) 方面的发展而获得1908年诺贝尔物理学奖 (Nobel Prize in physics)。

关于庞加莱的讲座和他对实验的态度，莫里斯·多卡涅 (Maurice d’Ocagne) (1862–1938) 有一段富有启发性的记述。多卡涅是一位才华横溢的数学家和土木工程师，于1880年进入巴黎综合理工学院。从1893年起，他也在该校担任辅导员；他以皮埃尔·德利克斯 (Pierre Delix) 的笔名撰写文学随笔，还写了一部在巴黎大获成功的喜剧。他这样描述庞加莱关于物理与实验力学的讲座（引自 [Bellivier 1956]）：

不能说庞加莱是一位伟大的讲师；他高高在上地驾驭着听众，并不具备演说家 (orator) 的天赋。演示 (demonstrations) 效果也差强人意；人们明显感觉到他对仪器的构造和使用从未给予丝毫关注。当讲座期间这些仪器 (instruments) 中的一件被放在他的桌子上时，最有趣的莫过于看他试图使用它时那胆怯的样子。他带着惊讶的表情几次走近它，仿佛这种物质实现未能适应他头脑中那个清晰理解的纯粹示意图。他试图抓住他偶然碰到的几个螺丝，然后……他就放弃了。

也许庞加莱五岁时所患的瘫痪 (paralysis) 使他不自信，并在一定程度上妨碍了他的身体协调性。

数学物理的任命更偏理论，这使他有可能在许多领域扩展，无论是在讲学还是研究方面。每年，他都会为自己的讲座选择一个不同的主题，通常与他当时的兴趣相关。这些讲座被总结在由他的学生记录和编辑的笔记汇编成的书中，实际出版由理学院学生和校友友好协会 (Association amicale des élèves et des anciens élèves de la Faculté des Sciences) 组织。其中一些学生后来成名。每本书的最终文本都经过庞加莱的检查和批准。

在第4.5节，我们概述了这些数学物理的主题，在第11章，我们将更详细地讨论其中的一些。这些讲座主要关注理论物理 (theoretical physics)，但具有坚实的数学基础。数学物理学家通常要么局限于物理现象的数学背景，要么局限于数学理论的物理后果。庞加莱在这方面也是个例外，因为他在发展基础数学的同时，也考虑了物理含义。正如我们所见，他的天赋不仅仅是数学上的，他从小就表现出广泛的兴趣。

在他职业生涯的早期阶段，亨利·庞加莱的创造力必定已被广泛认可，因为在1887年1月31日，年仅32岁的他成为了法国科学院 (Academy of Sciences) 的成员。他获得了34票，超过了他的主要竞争对手、来自巴黎综合理工学院的阿梅代·曼海姆上校 (Colonel Amédée Mannheim) 的24票。曼海姆年长得多，并且当时不太喜欢学生时代的亨利·庞加莱。

对许多科学家来说，被任命为科学院院士是成功科研生涯的顶峰，但对庞加莱来说，这仅仅是个开始。瑞典国王奥斯卡二世 (King Oscar II of Sweden) 曾设立奖项，奖励关于几个可选主题（其中之一是太阳系的稳定性 (stability of the solar system)）的最佳科学论文。庞加莱凭借其贡献在1889年获得了一等奖；见第五章。他的朋友阿佩尔获得第二名。

著名天文学家费利克斯·蒂塞兰 (Félix Tisserand) (1845–1896) 于1896年去世，庞加莱接替他担任数学天文学和天体力学 (mathematical astronomy and celestial mechanics) 教席。在1892–1899年期间，庞加莱出版了三卷关于天体力学新方法的著作 [Poincaré 1892]；亦见本书第9.3节。尽管这些书以天体力学，即引力场 (gravitational field) 中质点运动的研究为出发点，但它们可以被认为是动力系统 (dynamical systems) 的首次现代处理。这些书中发展的概念和方法具有超越用于阐释理论的天体力学具体问题的形式和普适性。五十年前，卡尔·古斯塔夫·雅可比 (Carl Gustav Jacobi) 在动力学领域取得了巨大进步。利用雅可比的工作，庞加莱提出了一种全新的方法，涉及变分方法 (variational methods) 和线性化方法 (linearization methods)、积分不变量 (integral invariants) 以及周期解 (periodic solutions) 和其他类型的特殊解。

4.2 交往与旅行

对于现代科学家来说，前往科学会议 (conferences) 和研究中心 (research centres) 旅行，以及与同事 (colleagues) 进行定期的、往往是日常的接触，以进行激发性的讨论并了解各自领域的最新进展，是一种生活方式。大约在1900年，旅行既不像今天这样快捷也不简单，大部分科学联系是通过信件 (letters) 交流进行的。尽管如此，那个时代见证了国际会议 (international conferences) 的开端，庞加莱是常客。此外，庞加莱还被邀请到一些国外机构接受科学荣誉和奖项。他在国外科学院 (foreign academies) 的成员资格和荣誉博士学位 (honorary doctoral degrees) 多得无法在此一一列举。学位、荣誉和勋章列表可以在 [Lebon 1912] 中找到。

1906年，庞加莱当选为法国科学院 (Académie des Sciences) 院长，如上所述，他于1887年当选为该院院士。1908年3月5日，他成为享有盛誉的法兰西学术院 (Académie française) 的成员。该学会由红衣主教黎塞留 (Cardinal Richelieu) 于1635年创立，其主要使命是规范和推广法语 (French language)。这样的机构在世界上几乎是独一无二的，尽管西班牙 (Spain)、巴西 (Brazil)、俄罗斯 (Russia) 和瑞典 (Sweden) 也建立了受法兰西学术院某些理念启发的学院。该院只有40名成员，即“不朽者”(immortals)。庞加莱被任命接替因诗人苏利·普吕多姆 (Sully Prudhomme) 去世而空缺的第24号席位。在其欢迎辞中，院长弗雷德里克·马松 (Frédéric Masson) 提到庞加莱已经是35个学院的成员。在描述这位新晋不朽者的科学和哲学成就时，他强调法兰西学术院始终为科学家保留一席之地，以促进他们在澄清科学术语和短语的含义与用法方面的积极合作（关于马松演讲的详细记述见 [Lebon 1912]）。

我们现在简要讨论庞加莱的一些旅行和他参加的会议。我们之前提到了1897年在苏黎世举行的第一届国际数学家大会，会上庞加莱的全体报告由一位同事代读。1900年8月6日至12日，第二届国际数学家大会在巴黎举行，庞加莱担任主席 (chairman)。大会大约有40场讲座，包括希尔伯特 (Hilbert) 和米塔-列夫勒的论文。后者在他的讲座“魏尔斯特拉斯生活的一页”(Une page de la vie de Weierstrass) 中讨论了魏尔斯特拉斯 (Weierstrass) 和索尼娅·科瓦列夫斯卡娅 (Sonya Kovalevskaya) 之间的通信和联系。希尔伯特提出了他著名的将在二十世纪解决的数学问题清单 (list of mathematical problems)。第16个问题是“确定庞加莱先生方程 $d y / d x = f (x, y)$ （其中 $f (x, y)$ 是多项式 (polynomial)）的极限环的最大数量”。庞加莱在1908年再次提到了这个问题。第一次世界大战前的国际数学会议没有统一语言：意大利人 (Italians)、法国人 (French) 和德国人 (Germans) 使用各自的语言；米塔-列夫勒在法国讲法语，在德国讲德语。庞加莱的全体报告题为“论数学中的直觉与逻辑”(De l’intuition et de la logique en mathématiques)。除了一些小的改动，它完全包含在哲学著作 [Poincaré 1905b, 第一章] 中。庞加莱强调直觉 (intuition) 作为分析 (analysis) 和演绎 (deduction) 的补充。进一步讨论见第六章。

两年前，即1900年，庞加莱前往伦敦 (London) 领取英国皇家天文学会 (Royal Astronomical Society) 的金质奖章 (gold medal)。2月9日，在该学会的一次特别会议上，会长乔治·达尔文 (George Darwin) 向他致辞。在他的颂词 (eulogy) 中，达尔文指出庞加莱成功地研究了许多课题，但他的讲话重点关注了潮汐运动 (tidal motion) 理论和旋转流体质量 (rotating fluid masses) 的稳定性 [Lebon 1912]，这些也是达尔文本人研究过的课题。

1904年，为纪念（晚了一年）美国于1803年购买路易斯安那领地 (territory of Louisiana)，在美国密苏里州圣路易斯 (St. Louis, Missouri) 举办了一场大型国际世界博览会 (World’s Fair)——路易斯安那购地博览会 (Louisiana Purchase Exposition)，并计划同时举办一场国际艺术与科学大会。在十九世纪，新大陆 (New World) 仍然很少有国际知名的艺术家和科学家。博览会的组织者希望将这个在欧洲主要以拓荒者之地闻名的国家推向文化和科学的世界舞台。1903年，加拿大裔美国 (Canadian-American) 数学家兼天文学家 (astronomer) 西蒙·纽康 (Simon Newcomb) (1835–1909) 受委派邀请欧洲著名人士参加会议。他从法国邀请的人之一是亨利·庞加莱，后者在圣路易斯发表了一场关于数学物理原理的精彩演讲，预见了相对论 (relativity) 的一些概念。借此机会，他还遇到了美国天文学家兼数学家乔治·希尔 (George Hill) (1838–1914)，他了解并欣赏希尔在天体力学微分方程方面的工作。有一个未经证实的故事说，邀请他的大学教授问庞加莱想见谁。庞加莱只提到了一个名字，希尔，但这让教授们很尴尬，他们并不知道希尔，后者长期在一个非学术机构——航海年鉴办公室 (Nautical Almanac Office) 工作，而且相当隐居。

图4.2 加斯东·达布 (Gaston Darboux)，亨利·庞加莱的博士论文导师之一，后来的同事。

第四届国际数学家大会于1908年4月6日至11日在罗马 (Rome) 举行，有一百多场讲座。大会的一个新颖之处在于首次设立了专门讨论教育学 (pedagogy) 和应用数学 (applied mathematics) 的分会场，其中包括英国应用数学家贺拉斯·兰姆 (Horace Lamb) 和德国数学物理学家阿诺尔德·索末菲 (Arnold Sommerfeld) 的讲座。庞加莱没有出席在海德堡 (Heidelberg) 举行的第三届大会，但他前往罗马大会发表全体报告。不幸的是，他因前列腺疾病 (prostate condition) 病重。这是导致他1912年去世的疾病的最初迹象。他准备了一篇关于数学未来的演讲，由加斯东·达布 (Gaston Darboux)（见图4.2）代为宣读。该演讲内容基本收录在 [Poincaré 1908a, 第二章] 中。与原文的不同之处将在下一小节讨论。路易丝·庞加莱前往罗马陪伴丈夫；待他充分康复后，他们分阶段返回巴黎，每天只走相对较短的路程。

1905年和1910年，庞加莱两次前往布达佩斯 (Budapest)。1910年的旅程是为了大卫·希尔伯特 (David Hilbert) 从匈牙利科学院 (Hungarian Academy of Sciences) 领取博利亚伊奖 (Bolyai Prize)。庞加莱荣幸地负责报告希尔伯特的成就。1905年，庞加莱本人获得了博利亚伊奖（1901年投票决定），由该院成员古斯塔夫·拉多斯 (Gustave Rados) (1862–1941) 报告庞加莱的成就。这是该奖项首次颁发。拉多斯（见 [Lebon 1912]）强调了庞加莱在自守函数方面的成果，同时简要讨论了从天体力学到拓扑学 (topology) 的大量不同成果。

1909年，庞加莱应沃尔夫斯凯尔委员会 (Wolfskehl Committee) 邀请，在哥廷根 (Göttingen) 发表了六场讲座。这次机会让他得以会见同事费利克斯·克莱因和大卫·希尔伯特，但他仍在遭受前列腺问题的困扰。在准备1909年4月22日至29日这一周在哥廷根的讲座时，他写信给希尔伯特 [Poincaré 1999, p. 349]：

现在有一点我想提请您注意。我仍在经受去年在罗马遭遇事故的后果，我强烈需要采取某些预防措施。我不能喝酒，也不能喝啤酒，只能喝水。我不能出席宴会，也不能参加长时间的晚宴。

行程按计划进行。前三场讲座涉及积分方程 (integral equations) 及其物理应用；第四场是关于阿贝尔积分 (abelian integrals) 和福克斯函数。第五场讲座讨论了超限数 (transfinite numbers)（基数 (cardinal numbers) 和连续统假设 (continuum hypothesis)），而最后一场则讨论了新力学 (new mechanics)。在前五场讲座中，庞加莱用德语演讲，而在最后一场，他用法语演讲。新力学就是我们今天所说的狭义相对论 (special relativity)，我们将在第4.7节和第11.4节看到1909年人们对此的看法。

1911年见证了由比利时实业家欧内斯特·索尔维 (Ernest Solvay) 赞助、在布鲁塞尔 (Brussels) 举行的一系列历史性会议的开端。亨德里克·A·洛伦兹 (Hendrik A. Lorentz) 将主持前五届会议，据称他“机智而敏锐”。1911年的主题是辐射 (radiation) 和量子 (quanta) 理论。这是庞加莱和爱因斯坦 (Einstein) 第一次也是最后一次相遇。与会者注意到庞加莱多么积极地参与讨论，以及他对新兴的量子理论 (quantum theory) 多么感兴趣。

罗马关于数学未来的演讲

庞加莱1908年的原始演讲（可在国际数学联盟 (International Mathematical Union, IMU) 网站“Historic IMU/ICM”找到）在哲学著作《科学与方法》(Science et Méthode) [Poincaré 1908a] 中为更广泛的读者进行了润色和简化；关于算术 (arithmetic) 的部分减少了一半。在他的演讲中，庞加莱强调了线性和非线性变换的使用。他期望从不连续群 (discontinuous groups) 和闵可夫斯基 (Minkowski) 的数的几何 (geometry of numbers) 的应用中获得很多成果。我们在此简要讨论 [Poincaré 1908a] 中省略的主题。

关于微分方程，对非线性方程的了解还很少。考虑奇点邻域会给出初步分类，使用变换群可能发挥有益作用，就像对代数曲线 (algebraic curves) 使用双有理变换 (birational transformations) 一样。考虑一阶方程 $d y / d x = f (x, y)$ ，我们甚至对积分 $F (x, y) =$ 常数了解不够。我们不知道积分的何种参数化 (parameterization) 也能满足微分方程。了解一阶方程中可能的极限环数量对于定性洞察至关重要。

数学物理中的大多数偏微分方程 (partial differential equations) 是线性的。弗雷德霍姆 (Fredholm) 的无穷行列式 (infinite determinants) 理论对此非常有帮助。结合希尔伯特推进的狄利克雷 (Dirichlet) 变分方法 (variational approach)，这项研究将继续进行。庞加莱指出，结合这两种方法并不容易，并且他也质疑这种结合是否能带来很多好处。

阿贝尔函数 (abelian functions) 的理论现在可以认为已经完成；有些与积分和代数曲线相关，有些与积分和流形 (manifolds) 相关。

在（复）函数 (complex functions) 理论中，单变量函数和多变量函数之间存在本质区别。我们关于两个变量的有理函数的知识对于更多变量的超越函数 (transcendental functions) 意味着什么尚不清楚。像单复变函数那样进行的单值化（见第八章）是否可以推广到更多变量？

庞加莱认为群论 (group theory) 是一个非常广泛的领域，并将自己局限于李群 (Lie groups) 和伽罗瓦群 (Galois groups)。李群理论已取得长足进步，现在应该提供更简单的证明和结果分类。在伽罗瓦理论 (Galois theory) 中进展不大。与李理论的并行性应该有所帮助。

4.3 保罗·阿佩尔

本节专门更详细地讨论亨利·庞加莱的朋友保罗·埃米尔·阿佩尔 (Paul Émile Appell)（1855年9月27日–1930年10月24日），我们在前几章已经见过他。保罗·阿佩尔（见图4.3）出生在阿尔萨斯 (Alsace) 的斯特拉斯堡 (Strasbourg)，这是法国和德国之间长期存在争议的领土。他的父亲让-皮埃尔·阿佩尔 (Jean-Pierre Appell) 是里特鲁斯 (Ritterhus) 的一名染工 (dyer)，大部分家人都从事这个行业。1870年，阿尔萨斯被普鲁士吞并，阿佩尔一家搬到南锡以保留法国国籍。保罗就读于南锡高级中学，如前所述，他在那里遇到了亨利·庞加莱，两人结下了终生的友谊。

1873年，保罗和亨利搬到巴黎继续学业，保罗就读于巴黎高等师范学院 (École Normale Supérieure)，1876年以第一名的成绩毕业。1881年，他娶了阿梅莉·贝特朗 (Amélie Bertrand)，她是数学家约瑟夫·贝特朗 (Joseph Bertrand) 和

图4.3 保罗·阿佩尔

查尔斯·埃尔米特 (Charles Hermite) 的侄女，也是埃米尔·皮卡 (Émile Picard) 的表妹。1885年，他成为巴黎索邦大学的力学教授，1892年当选为法国科学院院士。从1903年到1920年，他担任索邦大学理学院院长 (dean)，从1920年到1925年，他担任该大学校长 (rector)。此外，他一生中还担任过许多重要的公职。1925年，他出版了亨利·庞加莱的传记 (biography) [Appell 1925a]。在第七章，我们引用了该传记中他的一些评论。在巴黎的晚年，阿佩尔和庞加莱有很多机会在索邦大学交谈，常常是在下班回家的路上。他们的合作并非以合著论文或书籍的形式出现，而是持续的讨论和思想交流。

保罗·阿佩尔撰写了数百篇关于分析、几何和力学的文章和书籍。他对问题的把握和解决问题的方法都非常出色，但他的才能更多地体现在解决问题上，而不是发展一般理论。这种对推广 (generalization) 和抽象 (abstraction) 缺乏兴趣可能就是他今天不如他同时代某些人知名的原因。他自己编纂的出版物概览 [Appell 1925b] 远非完整。我们描述他的一些卓越成就。

1880年，他构造了所谓的阿佩尔多项式 (Appell polynomials) [Appell 1880]。这些是非常通用形式的复多项式。作为特例，它们包含了伯努利多项式 (Bernoulli polynomials)、埃尔米特多项式 (Hermite polynomials) 和拉盖尔多项式 (Laguerre polynomials)。由泛函方程 (functional equations) 和微分方程隐式定义的解析函数的展开可以用阿佩尔多项式来进行。现代推广，保罗·阿佩尔已经探索过的，是双变量多项式展开 (two-variable polynomial expansions)，它们是经典（雅可比 Jacobi）正交展开 (orthogonal expansions) 的类似物。

一个结合几何学和力学的巧妙方法涉及将平面进行到自身的单应变换 (homographic transformation)。这种阿佩尔变换 (Appell transformation) 可以用来 [Appell 1891] 确定作用在平面上质点上的力，这些力产生圆锥曲线 (conic sections) 作为轨迹（贝特朗问题 Bertrand’s problem）。

吉布斯-阿佩尔方程 (Gibbs–Appell equations)，早先由吉布斯 (Gibbs) 考虑过，构成了描述动力学中完整约束系统 (holonomic systems) 和非完整约束系统 (nonholonomic systems) 的另一种方式 [Appell 1900]。对于完整约束情况，它们等价于力学的拉格朗日方程 (Lagrange equations)，但由于它们包含了非完整约束情况（带约束 (constraints) 的系统，例如在表面上运动的陀螺），它们代表了经典力学 (classical mechanics) 微分方程的一种非常普遍的表述（亦见 [Appell 1921, Vol. 2]）。

关于力学及相关数学的非常完整的论述，也许是二十世纪科学文献中最完整的，可以在阿佩尔的四卷本《理论力学教程》(Traité de Mécanique Rationelle) [Appell 1921] 中找到。它也是一个丰富的参考文献来源。第一卷论述静力学 (statics) 和动力学 (dynamics) 的基本理论，包括许多经典例子。第二卷讨论质点系 (systems of mass points) 理论，主题包括积分不变量和非完整约束系统。除了通用理论，还有大量关于摆 (pendulums)、碰撞 (collisions) 和工程问题的应用。第三卷考虑连续介质 (continuous media) 的平衡 (equilibria) 和动力学，例如带不连续性 (discontinuities) 的波传播 (wave propagation)、流体力学 (fluid mechanics) 和弹性力学 (elasticity)。第四卷性质不同，侧重于旋转均匀流体质量在粒子间牛顿引力 (Newtonian attraction) 作用下的平衡态 (equilibrium states) 这一特定问题。这些问题与行星 (planet) 和恒星形成 (star formation) 理论相关。牛顿 (Newton) 已经观察到，以恒定角速度 (angular velocity) 绕固定轴旋转的流体质量应该产生一个两极扁平的椭球体形状 (ellipsoidal figure)。麦克劳林 (Maclaurin) 在1742年通过应用静水压力定律证明了这些椭球体确实是平衡图形；随后有许多其他科学家的贡献。1834年，雅可比将三轴平衡椭球体 (three-axial equilibrium ellipsoid) 加入到可能的平衡态中。这些椭球体绕其最短轴旋转。对于平衡态的稳定性，旋转速度是一个关键参数。该卷包含了对庞加莱发现的图形（亦见第11.2节）的描述，例如梨形图形 (pear-shaped figure) 和哑铃形图形 (halter)，以及稳定性计算。

4.4 与米塔-列夫勒的联系

庞加莱与瑞典数学家约斯塔·米塔-列夫勒（见图4.4）之间发展了一种特殊的关系，后者曾在巴黎师从埃尔米特，在柏林师从魏尔斯特拉斯。米塔-列夫勒的成长岁月使他对数学结果的表述采取了严谨的方法，因此毫不奇怪，他不喜欢庞加莱那种直观和非形式化的风格。但他无法忽视庞加莱论文中众多闪光的思想。两位数学家之间的通信始于1881年，直到1911年才结束；参见 [Nabonnand 1999]，以及完整的通信录 [Poincaré 2012] 和 [Poincaré 1999]，其中记录了259封信件。对两位数学家来说，如此大量的信件并不算特别，但通信持续时间之长，约三十年，则非同寻常。1881年的最初几封信——当时庞加莱还在卡昂——相当正式，但很快两人都采用了亲切的口吻；然而，除了 [Poincaré 1999] 中的第143封信，庞加莱在信中简短地谈到他母亲去世的悲痛之外，信件中很少涉及个人和私密的评论。

图4.4 约斯塔·米塔-列夫勒

在他们初次接触时，米塔-列夫勒已经是著名教授，是魏尔斯特拉斯最好的学生之一。像克莱因一样，他在与庞加莱的最初交流中采取了略带居高临下的口吻，但在了解到庞加莱的成就后，这种情况发生了改变。然而，即便在1883年，米塔-列夫勒仍写信给魏尔斯特拉斯：

您对庞加莱的第二篇论文“关于福克斯函数”(Sur les fonctions fuchsiennes) 有何看法？他不是德国大学的毕业生，确实令人遗憾。他的论文充满了新思想，但在我看来，它们在形式表述上还有太多需要改进的地方。

他在给埃尔米特的信中也提出了类似的抱怨（见 [Nabonnand 1999]），但事后看来，可以说试图强迫庞加莱采用魏尔斯特拉斯的风格，就像用赛马去拉牛车一样。考虑到庞加莱对巴黎综合理工学院数学教学的抱怨，这种尝试甚至可能使他完全疏远数学。尽管两位数学家风格迥异，但他们之间发展了长期的专业和友好关系。

1882年5月，米塔-列夫勒与来自赫尔辛基 (Helsinki) 的富家千金西格妮·林德福斯 (Signe Lindfors) 结婚。两位数学家的首次会面发生在这对瑞典夫妇的蜜月旅行之际，这次旅行的形式是访问欧洲的一些数学研究所，这引来了魏尔斯特拉斯如下的评论 [Poincaré 1999, p. 68]：

米塔-列夫勒夫妇上周在这里，从周三一直待到周日晚上。我经常见到他们。人们非常喜欢这位年轻女士；也欣赏她简洁却非常优雅的着装。米塔-列夫勒实际上进行了一次数学之旅——斯特拉斯堡、海德堡、哥廷根、莱比锡、哈勒 (Halle)、柏林——除了巴黎。对他来说当然很有趣——我不会说对那位年轻女士也是如此。

这对夫妇访问了巴黎，但——这是例外——不仅仅是为了数学原因。巴黎可能比他们访问的其他城市在文化上对西格妮更有吸引力，而且在个人层面上也令人满足，因为在这里她和她的丈夫第一次见到了亨利和路易丝·庞加莱。西格妮和路易丝彼此喜欢，这从 [Poincaré 1999] 的信件中可以清楚地看出。庞加莱曾数次前往瑞典，并在那里拜访了米塔-列夫勒，例如在1905年6月。

1882年，米塔-列夫勒写信给埃尔米特、阿佩尔和庞加莱，提出了一个新项目。他提议创办一份名为《数学学报》(Acta Mathematica) 的期刊，由他担任主编 (editor-in-chief)，并在编辑 (editors) 队伍中大量吸收德国和法国数学家。瑞典国王奥斯卡二世以及几个斯堪的纳维亚 (Scandinavian) 政府为该项目提供了资金支持。这后来被证明是数学界的一个重要项目。当时，数学研究的中心在德国，论文用德语撰写。法国也拥有杰出的数学家，其重要贡献用法文书写。然而，很少有德国人阅读法文，也很少有法国人阅读德文。此外，1870–1871年普法战争结束后，法国曾被普鲁士军队入侵，法国人明显变得仇德 (Germanophobic)。典型的是，庞加莱领先于克莱因在自守函数方面取得的大量成果，并不被认为是数学或科学的胜利，而被认为是法国的胜利。同样，法国科学家在国际竞赛中获奖也被认为是法国的征服，是对法兰西荣耀的贡献。当庞加莱和阿佩尔在1889年获得此类奖项时，他们两人都被授予了荣誉军团勋章 (Légion d’Honneur)。

结果是，像魏尔斯特拉斯、康托尔 (Cantor) 和施瓦茨这样的数学家的工作在法国相对不为人知，而埃尔米特、达布、拉盖尔和其他法国数学家的工作在德国也鲜为人知。一份来自像斯德哥尔摩 (Stockholm) 这样的中立地 (neutral place) 的新期刊，可以通过促成不同国籍数学家之间的编辑合作 (editorial cooperation) 来弥合这一鸿沟。

回想起来，对于这项事业，没有人比米塔-列夫勒更适合了。他曾在柏林师从魏尔斯特拉斯，在巴黎师从埃尔米特。他证明了自己是一位非常优秀的数学家，但完成这项智力装备的关键点在于他是一位天生的外交家 (diplomat)。在斯德哥尔摩，他通过为新成立的大学招募合适的人才而巧妙运作。他让瑞典国王对科学保持兴趣，并在全欧洲吸引了最优秀的数学家作为《学报》的撰稿人。《数学学报》最常用的语言是法语和德语。1883年，埃尔米特写信给瑞典驻法国大使说，《数学学报》是法国科学学院订阅的第一份外国科学期刊 [Poincaré 1999, p. 19]。毫无疑问，这封信是米塔-列夫勒建议的，以确保继续得到国王的支持。

米塔-列夫勒外交才能的另一个例子（众多例子中的一个）是他努力让庞加莱获得诺贝尔物理学奖。他试图争取瑞典物理学家 (Swedish physicists) 的支持，但这些人主要偏向实验 (experimentally oriented)，例如物理学家兼化学家 (chemist) 阿伦尼乌斯 (Arrhenius) (1859–1927) 就觉得庞加莱过于理论化 (theoretician) 而不予支持。作为营造理论家也有资格获奖氛围的第一步，米塔-列夫勒提名了亨德里克·A·洛伦兹 (1853–1928) 作为候选人。洛伦兹无疑是他那个时代最伟大的理论物理学家，他于1902年获得了诺贝尔奖，但却是与实验物理学家彼得·塞曼 (Pieter Zeeman) 共同获奖。这对诺贝尔委员会 (Nobel committee) 来说是一个转折点，但在很长一段时间里，他们仍然对偏重理论的物理学家持怀疑态度。米塔-列夫勒不惮于在他绝对不是专家的领域发表强硬意见。1908年，他在诺贝尔委员会中扭转了投票结果，将物理学奖授予了加布里埃尔·李普曼。候选人的提名由小组委员会准备，在一封给潘勒韦 (Painlevé) 的信中 [Poincaré 1999, p. 349]，他写道：

是我和弗拉格门 (Phragmén) 一起把奖颁给了李普曼。阿伦尼乌斯想把它给柏林的普朗克 (Planck)，但他那份在小组委员会获得一致支持通过的报告是如此愚蠢，以至于我能够摧毁它。最终，他只得到了13票（显然包括雷齐乌斯 Retzius），而我得到了46票。小组委员会的两名成员宣称，听了我之后，他们改变了看法，投票给了李普曼。我本不反对在维恩 (Wien) 和普朗克之间分享奖项，但单独把它给普朗克就是奖励那些仍然模糊不清、需要数学和实验来检验的思想。

古斯塔夫·雷齐乌斯 (Gustaf Retzius) (1842–1919) 是瑞典科学院著名成员，医学专家；威廉·维恩 (Wilhelm Wien) (1864–1928, 1911年诺贝尔奖) 和马克斯·普朗克 (Max Planck) (1858–1947, 1918年诺贝尔奖) 是杰出的物理学家。如果庞加莱没有在1912年英年早逝 (premature death)，米塔-列夫勒会继续他的努力。

《学报》的部分成功也要归功于庞加莱，他贡献了许多关于自守函数、天体力学和其他主题的长篇回忆录。其他法国数学家也做出了贡献，包括保罗·阿佩尔和加斯东·达布。魏尔斯特拉斯和康托尔的论文的德译法文版本也出现在《学报》上。总而言之，约斯塔·米塔-列夫勒对瑞典乃至整个欧洲科学组织的贡献是巨大而持久的。[Poincaré 1999] 中收录的通信也反映了围绕奥斯卡二世国王生日颁奖的私下且有时是痛苦的讨论；见第五章。在颁奖事件之后，[Poincaré 1999] 中的信件越来越多地涉及为《学报》编辑手稿的日常问题以及关于奖项和职位提名的讨论。

4.5 讲义与学生

庞加莱的讲义笔记 [Poincaré 1890a] 包含了数学和数学物理领域异常广泛的主题。三卷本的《天体力学新方法》(Les Méthodes Nouvelles de la Mécanique Céleste) [Poincaré 1892] 未包含在此列表中，因为它们不是常规教科书。这些卷册包含了一些天体力学 (celestial mechanics) 的应用，但其主要内容是发展了一套非常通用和基础的动力系统理论；见第9.3节。另一方面，三卷本的《天体力学讲义》(Leçons de Mécanique Céleste) 是为天文学家实际使用而编写的；它们是讲义笔记。在《讲义》的第二卷中，摄动函数 (perturbation function) 是用 [Poincaré 1892] 第一卷第六章讨论的方法发展的，但现在是针对实际的太阳系模型。这涉及到精妙的复分析。庞加莱指出，《讲义》中缺少 [Poincaré 1892] 的数学性和严谨性，但他旨在进行高精度的计算，实际上比当时观测所能达到的精度更高，但他期望观测会改进，需要更先进的计算。他还指出，与他自己关于数学方法的书 [Poincaré 1892] 一起，蒂塞兰 (1845–1896) 的旧书包含了对天体力学的极好介绍；庞加莱提到了这一点，并警告说他不打算重复 [Tisserand 1889] 四卷本中的章节。

1911年出版的关于宇宙起源学 (cosmogony) 理论的文本对庞加莱来说也是一个特殊的主题；它包含了对截至出版年份的所有宇宙起源假说的广泛批判性分析。他强烈支持拉普拉斯 (Laplace) 的星云假说 (nebula hypothesis)。更多细节可以在本书第11章找到。达布 [Darboux 1913] 指出，这项分析恰好停止在一个新的天文学分支——天体物理学 (astrophysics)，特别是光谱分析 (spectroscopic analysis)——出现之前，但它包含了对所有经典宇宙起源理论非常精确的评估和总结。在序言中，庞加莱写道，我们知之甚少的理论和进行的观测不足以让我们有真正的希望发展出一个可接受的理论。但是，“如果我们如此理性，如果我们只是好奇而没有不耐烦，我们可能永远不会创造科学，我们会一直满足于过我们渺小的生活。” 欧内斯特·勒邦 (Ernest Le Bon) 对庞加莱的工作和思想的有趣评价被添加到了宇宙起源学第二版中。其他一些主题，例如热传播和描述分岔现象的旋转流体质量平衡图形，将在第11章讨论。

除了基础的天体力学著作 [Poincaré 1892] 外，讲义笔记的书目细节在 [Poincaré 1890a] 中给出。这里我们列出讲义笔记的主题：

天体力学（《讲义》）
光的数学理论 (mathematical theory of light)，两卷
电学与光学 (electricity and optics)，两卷（麦克斯韦理论 (Maxwell theory) 和赫兹振荡 (Hertz oscillations)，无线电报 (wireless telegraphy)）
热力学 (thermodynamics)
弹性理论 (theory of elasticity)
涡旋运动 (“tourbillons” Vortical motion)
电振荡 (electrical oscillations)
毛细现象 (capillarity)
热传播解析理论 (analytical theory of the propagation of heat)
概率论 (probability)
位势论 (potential theory)
运动学 (kinematics) 与流体力学 (fluid mechanics)
流体质量的平衡图形 (equilibrium figures of a fluid mass)
宇宙起源假说 (cosmogonic hypotheses)

索邦大学的讲座及相应书籍的理念是以拉普拉斯和柯西 (Cauchy) 的精神来呈现数学物理。这意味着从几个物理假设出发，尽可能完整地发展相应的理论，即获得物理现象的理论解释并将其与实验进行比较。天体力学和位势论的处理是这种方法的典型，因为现象的物理本质，即引力 (gravitation)，可以通过经典力学得到很好的描述。对于物理学中较新的部分，其基础仍在研究和讨论中，这更加困难，但仍然可以作为理想。在这方面，庞加莱对麦克斯韦 (Maxwell) 的表述持相当批判的态度，他说麦克斯韦的思想令人钦佩，但同时又重点不明，缺乏系统的理论构建。达布 [Darboux 1913] 同意这一观点，但指出约瑟夫·贝特朗 (1822–1900) 不同意。达布引用庞加莱关于麦克斯韦工作的评论：

也许有一天，物理学家将对那些实证方法无法触及的问题不感兴趣，并将它们留给形而上学家 (metaphysicians)。这一天还没有到来；人类不会轻易地甘于对探究领域的基础保持无知。

在第4.6节，我们更详细地介绍了庞加莱对麦克斯韦的批评。

由于庞加莱对天体力学的兴趣，人们可能会产生一种肤浅的印象，即他关于微分方程的工作主要涉及常微分方程。然而，正如讲义笔记的标题已经表明的那样，在相当多的讲座中，庞加莱使用并发展了偏微分方程。其中有许多原创结果，例如关于拉普拉斯方程和泊松方程 (Poisson equation)、扫除法 (balayage methods) 和波动方程 (wave equations)；见第11章。

最引人注目的是其产生的大量工作。实际的讲学时期涵盖了非常不同的主题，例如：

1888–1889：电学与光学，第一部分
1889–1890：电学与光学，第二部分
1891–1892：第二学期，涡旋运动 (“tourbillons” vortex motion)
1893–1994：第一学期，热学理论 (theory of heat)
1893–1994：第二学期，概率论

这些讲座对当时法国学生的教育影响必定是巨大的。笔记由学生编辑（见 [Poincaré 1890a]）并最终由庞加莱批准。一些学生后来声名鹊起；我们提到埃米尔·博雷尔 (Émile Borel) (1871–1956)、儒勒·德拉赫 (Jules Drach) (1871–1949) 和勒内·贝尔 (René Baire) (1874–1932)。有趣的是，托比亚斯·丹齐格 (Tobias Dantzig) (1884–1956) 当时正在巴黎学习数学。他出生在拉脱维亚 (Latvia)，在巴黎学习并结婚，1910年移民到美国。他于1917年获得数学博士学位，是美国数学家乔治·丹齐格 (George Dantzig) (1914–2005) 的父亲，后者因其在线性规划 (linear programming) 方面的工作而闻名。

大约在1900年，甚至直到二十世纪中叶，在法国撰写博士学位论文 (doctoral dissertation) 都是一件孤独的事情，博士生与指导教授只有偶尔的接触。当论文完成时（或者如果学生认为已经完成），它会被提交给一个委员会 (committee) 进行分析和评判。如果论文获得“最优”(très honorable) 等级，其作者很有可能随后在索邦大学获得职业生涯。有三位数学家，庞加莱显然在他们的博士工作指导中扮演了重要角色。众所周知的是路易·巴什利耶 (Louis Bachelier) (1873–1946)，他在1900年提交了一篇关于投机理论 (theory of speculation) 的论文（见图4.5）。凭借其关于买卖股票 (equities) 的概率后果的成果，它远远领先于时代。在金融经济学 (financial economics) 领域，巴什利耶的工作在他去世后才得到认可。在他的委员会报告中，亨利·庞加莱称该主题不寻常，但指出该工作质量很高。尽管这篇论文荣幸地发表在著名的《巴黎高等师范学院科学年鉴》(Annales Scientifiques de l’École Normale Supérieure) 上，巴什利耶的职业生涯远非一帆风顺。他最终在贝桑松大学 (University of Besançon) 获得了永久学术职位。

图4.5 路易·巴什利耶 (1873–1946)，金融数学奠基人之一，庞加莱的学生

庞加莱不仅是一位异常有天赋的科学家；在他对主题的兴趣和选择上，他也可能不落俗套。他支持并指导了巴什利耶在金融数学方面的工作。此外，他的学生 A. 基凯 (A. Quiquet)，编辑了庞加莱关于概率论的讲义笔记（见 [Poincaré 1890a]），致力于精算 (actuarial) 和统计经济问题 (statistical economic problems)。1906年3月，米塔-列夫勒请庞加莱联系基凯，以获取有关成立瑞典精算学会 (Swedish actuarial society) 的信息。不出所料，米塔-列夫勒成为了该学会的主席 [Poincaré 1999, 信件 227]。几周后庞加莱的回复包含了必要的信息。

与庞加莱相关的第二位博士生是塞尔维亚人 (Serbian) 米哈伊洛·彼得罗维奇 (Mihailo Petrović) (1868–1943)，他于1894年撰写了一篇关于微分方程的论文；除了庞加莱，数学家埃尔米特、皮卡和潘勒韦 (Painlevé) 在决定其内容方面也发挥了作用。彼得罗维奇（见图4.6）回到贝尔格莱德 (Belgrade)，成为塞尔维亚有影响力的科学家。

图4.6 米哈伊洛·彼得罗维奇 (1868–1943) 撰写了一篇关于微分方程的论文

罗马尼亚人 (Romanian) 迪米特里·蓬佩乌 (Dimitrie Pompeiu) (1873–1954)，见图4.7，于1905年因其在复函数理论方面的工作获得博士学位，后来成为罗马尼亚的领军数学家。

4.6 法英风格之争

在关于电学与光学的讲义笔记 [Poincaré 1890a, nr. 2]，《电学与光学》(Electricité et optique) 中，引言与麦克斯韦发展理论物理的风格划清了界限。开头如下：

当一位法国读者第一次打开麦克斯韦的书时，一种沮丧甚至常常是怀疑的感觉与钦佩混合在一起。只有经过长期的努力和付出巨大的代价，这种感觉才会消失。一些杰出的头脑将永远保持这种感觉。

为什么这位英国科学家的思想如此难以在我们这里扎根？这无疑是因为大多数受过教育的法国人的教育使他们首先追求精确性和逻辑性。

数学物理的旧理论在这方面给了我们完全的满足。我们所有的导师，从拉普拉斯到柯西，都采用了相同的方式。从明确表述的假设出发，他们从中严格地推导出结论，然后将它们与实验进行比较。似乎他们想让物理学的每一个分支都具有与天体力学相同的精确性。

在痛惜麦克斯韦著作中缺乏逻辑连贯性和抽象性之后，庞加莱指出，“麦克斯韦没有给出电和磁的力学解释；他仅限于证明这种解释是可能的。”庞加莱指出麦克斯韦的构造是初步的，并且彼此独立。假设之间的关系不清楚。一些结果是矛盾的。在一个坚实的电学、磁学和光学理论中，应该能够识别可观测变量 (observable variables)，并为相关量建立拉格朗日运动方程 (Lagrangian equations of motion)。这样一个系统地发展并经过经验检验的理论，才会被认为是自然现象的解释。

图4.7 迪米特里·蓬佩乌 (1873–1954) 撰写了一篇关于复函数理论的论文

有趣的是，这种英国式的数学物理风格一直持续到二十世纪中叶。它也影响了美国科学家，直到1930年代在欧洲大陆移民的影响下，美国理论物理学才发生了理性化。二十世纪下半叶科学的高度国际化极大地缩小了科学风格的差异，但差异并未完全消失。

4.7 相对论：新力学

关于新力学，即用相对论 (relativity) 取代牛顿经典力学 (Newtonian classical mechanics) 的主要优先权争议 (priority controversy) 围绕着狭义相对论 (special relativity)，主要候选人是爱因斯坦 (Einstein)、洛伦兹 (Lorentz) 和庞加莱。运动的相对性本身早已由伽利略 (Galileo) 和惠更斯 (Huygens) 研究和阐述，但仍然假设存在一个绝对的运动参考系 (absolute reference frame)。其观点在1900年左右进行的实验显示光速 (velocity of light) 与观察者选择的惯性系 (inertial system) 无关之后发生了巨大变化。亨德里克·洛伦兹 (1853–1928) 将光速在每个惯性系中的这种恒定性作为其力学的基础。这是可以观测到的最大速度，为了容纳这一点，他做出了一个绝妙的假设，即物体的大小和质量取决于在给定惯性系中的速度。他提出的所谓洛伦兹收缩 (Lorentz contraction) 公式明确给出了这种关系。此外，洛伦兹引入了局部时间 (local time) 的基本概念，即时间依赖于在给定惯性系中的位置和速度。因此，像大小和质量一样，时间没有绝对意义；不存在绝对的运动参考系。

庞加莱早在1900年就指出，辐射 (radiation) 可以被视为具有等效质量 (equivalent mass) 的虚拟流体 (fictitious fluid)；亦参见 [Poincaré 1908a] 和第11.3节中对这些思想的讨论。他从洛伦兹的“电子理论”(theory of electrons) 中推导出这种解释，该理论包含了麦克斯韦的辐射压力 (radiation pressure)。当然，值得注意的是，庞加莱在引用他人时总是准确甚至慷慨，但在他1909年的讲座中（见第11.4节）却没有提到爱因斯坦。这说明当时许多物理学家和数学家认为洛伦兹是新力学理论（现称狭义相对论）的主要贡献者。典型的是，即使在1913年，达布仍然写道 [Darboux 1913]，庞加莱讨论了“洛伦兹的力学”(mechanics of Lorentz)。然而，有迹象表明，洛伦兹认为他的观察是临时的假设，而爱因斯坦则提出了一个完整而全新的物理实在观，尤其是在1916年他阐述广义相对论 (general relativity) 理论时。1927年，洛伦兹 [Lorentz 1928] 在一次会议上这样阐述了优先权问题：

我仅将我的时间变换视为一种启发式的工作假设。因此，相对论确实完全是爱因斯坦的工作。毫无疑问，即使该领域所有前辈的工作都未完成，他也会构思出它。在这方面，他的工作独立于先前的理论。

这也许过于慷慨了。如果将“启发式”解读为“方便的”，那么狭义相对论的大部分要素都存在于洛伦兹的力学中；后来，爱因斯坦将新力学扩展到了广义相对论。

庞加莱和洛伦兹在他们的著作中将以太 (ether) 作为既定事实提及，表现出一种矛盾心理。他们似乎不愿意忽略它或摆脱它；关于庞加莱提及以太，例如参见 [Poincaré 1902] 中的随笔“现代物理学理论”(Theories of Modern Physics) 和 [Poincaré 1905b] 中的“科学与实在”(Science and Reality)。在他的演讲 [Lorentz 1915] 中，洛伦兹这样说：

为什么我们不能谈论以太而不是真空 (vacuum)？空间和时间是不对称的；一个质点可以在不同时间处于同一点，但不能在同一时间处于不同地方。

在 [Borel 1914, 注III] 中，博雷尔在庞加莱关于“空间的相对性”(relativity of space) 的讨论中注意到了类似的模糊性。根据博雷尔的说法：

因此，或许有必要澄清，他关于空间相对性的思想是形而上学家而非科学家的思想：庞大的科学体系并未增加对外部物体存在的形而上学怀疑 (metaphysical doubt)。

尽管如此，在讨论优先权时，洛伦兹对狭义相对论理论阐述的基础性贡献，例如他的变换公式和局部时间概念，应与庞加莱的贡献，即他对洛伦兹群 (Lorentz group) 和相对性原理 (principle of relativity) 的阐述一起得到承认；见第11.3节。在某种程度上，洛伦兹1927年的上述表述应该补充他对庞加莱“电子动力学”(dynamics of the electron) 论文的评价，见 [Lorentz 1914, p. 298]：

另一方面，庞加莱获得了电动力学方程的完美不变性，并且他用他首先使用的术语阐述了“相对性假设”(relativity postulate)。

1915年在阿姆斯特丹皇家科学院 (Royal Academy of Sciences, Amsterdam) 的一次演讲中，洛伦兹是这样说的 [Lorentz 1915]：

我可以向你们指出 [如果我有更多时间的话] 庞加莱在他关于电子动力学的研究中，大约在与爱因斯坦同一时间，阐述了许多对其理论具有特征性的思想，并且还阐述了他称之为“相对性假设”(le postulat de relativité) 的内容。

在这方面，很难理解为什么爱因斯坦在1949年描述相对论发展时 [Einstein 1950]，提到了许多科学家，特别是洛伦兹，却省略了庞加莱。

4.8 社会参与

即使在很小的时候，亨利·庞加莱就对他所在的城镇、国家和世界上发生的事情感兴趣。这不仅从他的信件和与朋友的交谈中可以清楚地看出；也出现在他的讲座和著作中。1886年，他协助父亲莱昂在南锡组织了一次关于科学进步的大会。后来，他在《科学总汇评论》(Revue Générale des Sciences) 上发表关于科学的科普文章。他的哲学随笔，大部分已出版在四本书中（见第六章），涉及心理学 (psychology)、教育 (education)、数学基础 (foundations of mathematics) 和自然科学 (natural sciences)。政治 (politics) 话题也未回避。

在 [Poincaré 1911] 中，庞加莱讨论了科学与人文学科 (humanities) 之间的关系，这里自然涉及到了教育。1912年，应“文理中学之友”(friends of the gymnasium) 的请求，他访问了维也纳 (Vienna)，谈论文理中学 (gymnasium) 在教育中的未来。以下引自 [Poincaré 1911]：“科学有奇妙的应用，但只着眼于应用的科学将不成其为科学；它将不过是厨房而已。”同样在1912年，庞加莱发表了一篇关于接受人与人之间的差异以及避免不同社会群体之间仇恨的必要性的演讲（见第十二章）。保罗·阿佩尔 [Appell 1925a] 写道，1904年，《蓝色评论》(La Revue Bleue) 期刊寻求对政治感兴趣的科学家的参与。对于编辑的请求，庞加莱回答说：

你问我对政治感兴趣的科学家应该反对还是支持政府。好吧，这次我得推辞了；每个人都必须根据自己的良心来选择。我认为并非每个人都会投同样的票，我看不出有什么理由对此抱怨。如果科学家参与政治，他们应该参与所有党派，而且他们确实有必要出现在最强大的党派中。科学需要资金，不应该让当权者说，科学，那是敌人。

1904年，在同一份期刊《蓝色评论》上，他发表了对政治中比例代表制 (proportional representation) 的看法。选举制度 (electoral systems) 在那个时代经常被讨论，例如约瑟夫·贝特朗在概率论的背景下讨论过。在 [Poincaré 1913] 中，庞加莱讨论了伦理 (ethics) 与科学的关系，宗教道德 (religious morality) 与科学道德 (scientific morality) 之间的对比，后者涉及科学家的情感心理学。

很明显，庞加莱常常直言不讳地表达自己的观点，但他不想成为任何人的工具。当然，当他成名后，这种尝试是有的。他在社会问题上表达得非常谨慎，同时又不失明确。例如，这可以从他1912年为法国道德教育联盟 (Ligue française d’éducation morale) 所作的精彩演讲“为社会宽容辩护”（第十二章）中看出。

在德雷福斯事件 (Dreyfus affair) 问题上也可以观察到这一点，该事件在1900年左右使法国陷入了一场社会危机 (social crisis)。由于其对法国发展乃至其在整个欧洲影响的巨大后果，我们更详细地描述这些事件。

德雷福斯事件

十九世纪末，一场重大的政治和社会危机席卷法国：陆军上尉阿尔弗雷德·德雷福斯 (Alfred Dreyfus) 的审判和定罪事件。科学在这场悲剧中扮演了一个次要但决定性的角色，它被用来在1894年的第一次审判中获取德雷福斯有罪的“证据”。当获得重审时，一个由三名科学家组成的委员会——科学院常任秘书 (permanent secretary) 加斯东·达布；科学院院长亨利·庞加莱；以及科学院院士兼索邦大学理学院院长的保罗·阿佩尔——被要求就实际上是控告关键部分的科学推理提交报告。这位上尉的审判和重审在现代历史上在几个方面是独特的，因为它在社会中引发了情感的冲击波；它引发的讨论、文章和书籍；以及对个人的许多后果，涉及失业、监禁，在一些案例中甚至导致谋杀或自杀。即使在今天，讨论该事件在某些法国军队圈子里仍然会引起麻烦。为了理解科学委员会的工作，我们回顾一下该事件的主要经过（亦见 [Birnbaum 1994]）。

事件的开端

1894年12月，法国军队的一位年轻犹太 (Jewish) 军官阿尔弗雷德·德雷福斯被判犯有叛国罪 (high treason)。他被军队开除，军刀被当众折断，并被终身流放到法属圭亚那 (French Guiana) 附近的魔鬼岛 (Devil’s Island) 监狱岛。四年后，小说家兼政论家埃米尔·左拉 (Émile Zola) 写下了他著名的《我控诉》(J’accuse)，在文中他宣称德雷福斯无辜，同时指控军事机构粗暴违反司法规则。这篇文章在法国引起了巨大的骚动，将国家分裂成两个派别：呼吁“为德雷福斯伸张正义”的德雷福斯派 (Dreyfusards)，以及为当权派特别是军队的行为辩护、有时爆发出可怕的反犹主义 (anti-Semitism) 情绪的反德雷福斯派 (anti-Dreyfusards)。

当时，法德关系紧张。在1870–1871年的普法战争期间，普鲁士军队占领了法国部分地区。1871年签署的和平条约对法国不利，法国东部大片领土割让给了德国。由于在军事学校的出色表现以及随后在军队中的职业生涯，德雷福斯上尉于1893年被调入总参谋部 (General Staff)。这并不像现在看起来那么简单。法国军官阶层由贵族出身、信奉天主教 (Catholic) 且拥护君主制 (royalist) 的军官主导。当德雷福斯被考虑担任这样一个职位时，选拔委员会的一位将军因为他是犹太人而将他的名字从考虑名单中移除。德雷福斯提出的官方抗议——“难道犹太军官不能像其他人一样为国效力吗？”——说服了委员会，认为他适合这个职位。

1894年，法国人在一名德国军官的物品中发现了一份包含法国军事机密信息的文件。信息必定来自总参谋部办公室，据此断定那里有一名间谍 (spy) 活动。根据法国军队反情报部门 (counterintelligence) 的说法，这只能是在那里工作的犹太军官，德雷福斯立即被捕。在审判准备过程中，警察局（检察官办公室 the bureau of the prosecuting attorney）研究科科长阿尔方斯·贝蒂荣 (Alphonse Bertillon) 发挥了关键作用。贝蒂荣涉猎笔迹学 (graphology)，并有一些非常怪异的想法。罪证文件上的笔迹与德雷福斯的不像，这一点被贝蒂荣认定为自我伪造 (autoforgerie)。根据他的报告，他伪装笔迹这一事实更有力地证明了德雷福斯是一个非常老练的间谍。

审判后，当德雷福斯在魔鬼岛受苦时，他的兄弟马蒂厄 (Mathieu) 非常活跃。他接触政治和法律权威，请求复审程序，并获取新信息以证明他兄弟的清白。他发现了一些显著的法律违规行为，媒体再次对此案产生兴趣。此外，文件上的笔迹被确认为总参谋部另一位军官费迪南·瓦尔辛·埃斯特哈齐 (Ferdinand Walsin Esterhazy) 的。事实证明，埃斯特哈齐一直在向德国人出卖关于法国军队的信息，并在1898年底匆忙离开法国。

与此同时，对德雷福斯无罪证据的反应是狂怒的。反德雷福斯派的民族主义大规模示威活动几乎在每个法国城镇都发生了。大约10,000人在巴黎示威，反德雷福斯和反犹口号十分醒目。大多数神职人员、宗教团体甚至梵蒂冈 (Vatican) 都支持反德雷福斯派。有趣的是，即使在第二次世界大战后，当审查支持纳粹 (Nazi) 的维希政权 (Vichy regime) 的宣传时，仍然可以找到对这些事件的提及。

科学委员会

根据司法命令，第一次审判中使用的证据由来自法国科学院的三位科学家组成的委员会进行了复审，该委员会由达布、庞加莱和阿佩尔组成。就其本身而言，选择这样一个委员会并不能保证评估的公正性。科学院过去是、现在显然也是当权派的一部分，因此不仅是一个科学机构，也是一个政治机构。例如，当爱因斯坦于1922年访问巴黎进行一些讲座时，人们担心会发生民族主义示威。爱因斯坦是德国人！一次为科学院组织的讲座在30名院士，包括其院长，宣布将抵制该活动后被取消了。

然而，审查德雷福斯案证据的委员会证明是公正的，并且在其报告的所有细节上完全一致。当得知德雷福斯是根据辩方不知道的证据被定罪时，庞加莱对阿佩尔说 [Appell 1925a]：“指控的严重性可能摧毁了法官的批判意识。”该委员会被要求审议贝蒂荣的笔迹分析，该分析与一项概率计算相关联。庞加莱作为委员会主席在给法庭的信中写道：“这项证据中没有任何科学性，我无法理解你们的不安。我不知道被告是否会被判有罪，但如果是，那将是基于其他证据。不可能这样的论证会被受过科学教育且没有偏见的人严肃考虑。”阿佩尔指出，在整个过程中，庞加莱因提交给委员会的问题的琐碎性而表现出一定的不耐烦。尽管如此，他还是认真地考虑了这些问题并给予了充分的关注。

根据阿佩尔 [Appell 1925a] 的说法，庞加莱在这些诉讼过程中的态度是他对公共道德看法的典型体现。这在1912年的一次演讲中以更普遍的背景表达出来，他在演讲中评论了人与人之间的差异，并讨论了社会中的仇恨；见第十二章。

重审、赦免和平反

1899年，应其妻子露西 (Lucie) 的请求，德雷福斯获得了法律程序的复审，并在雷恩 (Rennes) 军事法庭 (military court) 进行了重审。违背所有逻辑和理性，德雷福斯再次被判有罪，这次判处十年监禁 (imprisonment)。然而，由于健康状况不佳，德雷福斯请求共和国总统埃米尔·弗朗索瓦·卢贝 (Émile François Loubet) 赦免 (pardon) 他。总统于同年批准了赦免。

1903年，政治家让·饶勒斯 (Jean Jaurès) 重新开启此案。负责官员发现了更多伪造的证据，1906年，一家高等法院在第三次审判中裁定对德雷福斯的指控没有任何根据。他被恢复军职并被授予荣誉军团勋章。他的遗言是：“我只是一名炮兵军官 (artillery officer)，因一次悲剧性的错误而被阻止了我的职业生涯。”

第五章奥斯卡二世奖竞赛

1885年夏天，几家科学期刊上刊登了一则奖项竞赛的公告。该公告来自约斯塔·米塔-列夫勒 (Gösta Mittag-Leffler)，声明瑞典和挪威国王奥斯卡二世 (King Oscar II of Sweden and Norway) 决定赞助一项科学竞赛，奖品将于1889年1月21日，即他60岁生日时颁发。竞赛的实际操作由三名委员会成员负责：主席约斯塔·米塔-列夫勒（斯德哥尔摩 Stockholm）、卡尔·魏尔斯特拉斯 (Karl Weierstrass)（柏林 Berlin）和查尔斯·埃尔米特 (Charles Hermite)（巴黎 Paris）。奖品包括一枚金质奖章 (gold medal) 和2500克朗 (kronor) 奖金。参赛回忆录须于1888年6月1日前提交。

参赛者可以从四个主题中选择。亨利·庞加莱 (Henri Poincaré) 选择的第一个主题，表述如下（见 [Barrow-Green 1997]）：

给定一个由任意数量粒子组成的系统，粒子间根据牛顿定律 (Newton's law) 相互吸引，假设永远不会发生两个粒子的碰撞 (impact)，要求将每个粒子的坐标展开为级数 (series)，该级数按照时间的某些已知函数进行，并且在任何时间段内一致收敛 (converging uniformly)。

这个问题，其解决将极大地扩展我们对宇宙系统 (system of the universe) 的知识，似乎可以用我们目前掌握的分析资源 (analytical resources) 来解决；这至少可以合理地推测，因为勒热讷-狄利克雷 (Lejeune-Dirichlet) 在去世前不久曾告知他的一位数学家朋友，他发现了一种积分力学 (mechanics) 微分方程的方法，并且他已经成功地应用这种方法，以绝对严格的方式证明了我们行星系统 (planetary system) 的稳定性 (stability)。不幸的是，除了发现的起点似乎是无穷小振荡 (infinitely small oscillations) 理论之外，我们对这种方法一无所知。然而，几乎可以肯定地推测，这种方法并非基于冗长复杂的计算，而是基于一个简单的基本思想的发展，人们有理由希望通过认真和不懈的研究再次找到它。

然而，如果在竞赛期间无人成功解决所提出的问题，奖项可能会授予一篇以指定方式处理并完全解决了力学中其他某个问题的著作。

回想起来，这种对狄利克雷陈述正确性的信任似乎很天真。这让人想起费马大定理 (Fermat's last theorem)，费马曾写道，他阐述该定理的书页边距太小，无法容纳证明。也许可以推测狄利克雷或费马确实掌握了这样一种方法或证明，但这似乎极不可能。此外，分配三年时间来解决一个至今仍完全未解决的问题，现在看来也颇为雄心勃勃。

在本章中，我们将描述竞赛的结果；一本包含更多细节和参考文献的专著是 [Barrow-Green 1997]。

5.1 克罗内克的评论与竞赛的开始

1885年奖项竞赛的公告引起了利奥波德·克罗内克 (Leopold Kronecker) (1823–1891) 给米塔-列夫勒的一封愤怒的信。说克罗内克不是魏尔斯特拉斯（见图5.3）的朋友，还是一种轻描淡写的说法，奖项委员会的组成显然让他感到恼火。除了对委员会组成和竞赛宣布方式的形式上的抱怨，克罗内克还有一个实质性的反对意见：委员会提出的第四个问题涉及与福克斯函数 (Fuchsian functions) 相关的代数问题。克罗内克声称他已经证明了公告中要求的结果无法实现。他威胁要就此点写信给国王。米塔-列夫勒辩称不知情，幸运的是，克罗内克没有再追究此事。

同年，1885年，克罗内克在一封给米塔-列夫勒的信中提出了关于问题一表述的疑问。他声称自己就是狄利克雷提到的那位“朋友”，因此，他是唯一能描述狄利克雷告诉他内容的人。三年后，即1888年，克罗内克公开了这一信息，并补充说狄利克雷的话被误引了。这很可能主要是对魏尔斯特拉斯的攻击，但整个委员会被期望做出反应。埃尔米特（见图5.1）不想卷入“这桩

图5.1 查尔斯·埃尔米特，奖项委员会成员

德国事务”(German affair)，而米塔-列夫勒和魏尔斯特拉斯则得出结论，除了省略了“朋友”的名字外，表述没有错误。他们决定无视克罗内克的攻击。

参赛者的身份本应保密，但庞加莱告诉了埃尔米特和米塔-列夫勒他打算提交一篇关于问题一的回忆录。到1888年6月竞赛截止时，共收到了十二份参赛作品，其中五份是关于问题一的。

5.2 委员会的活动与结论

米塔-列夫勒首先将十二份回忆录交给了年轻同事拉尔斯·爱德华·弗拉格门 (Lars Edvard Phragmén) (1863–1937)（见图5.2），任务是进行预选。到1888年夏初，他写信给魏尔斯特拉斯和埃尔米特，称只有三份参赛作品真正有价值，两份来自巴黎（庞加莱的和阿佩尔 Paul Appell 的）和一份来自海德堡。委员会仔细审查了这三份作品，并很快一致决定将奖项授予庞加莱。阿佩尔将获得荣誉提名奖。顺便说一句，保罗·阿佩尔选择了一个符合他自己口味的主题，即阿贝尔函数 (abelian functions) 的展开。

下一阶段对委员会来说要困难得多；需要对参赛作品进行公开评估，并将获奖回忆录发表在《数学学报》(Acta Mathematica) 上。与庞加莱的手稿常有的情况一样，证明中存在大量空白和许多直觉性的步骤。也可以有把握地说，奖项回忆录的全部内容及其陈述的有效性并未被委员会成员完全理解。那么他们如何能授予奖项呢？他们的立场由埃尔米特在给米塔-列夫勒的一封信中总结道 [Hermite 1985]（译文 [Barrow-Green 1997]）：

图5.2 拉尔斯·爱德华·弗拉格门，奖项回忆录的编辑

图5.3 卡尔·魏尔斯特拉斯，奖项委员会成员

庞加莱的回忆录具有如此罕见的深度和创造力，从分析及其对天文学后果的角度来看，它无疑将开启一个新的科学时代。但需要进行大量扩展的解释，目前我正在请求这位杰出的作者就几个要点给我指点。

埃尔米特可以询问作者，但庞加莱在回答他认为不言自明的陈述时仍然含糊其辞。然而，米塔-列夫勒采取了一个不同寻常的步骤，要求庞加莱为回忆录添加解释，这样就混淆了他作为奖项委员会主席和《学报》编辑的身份。庞加莱的回忆录本应占据《学报》158页，但他又额外增加了93页的注释。

奥斯卡二世国王在他生日那天，即1889年1月21日宣布，庞加莱赢得了奖项竞赛，阿佩尔获得了荣誉提名奖。法国报纸大肆宣扬这次法国的胜利，两位科学家都被法国政府授予了荣誉军团勋章。获奖回忆录连同阿佩尔的回忆录原定于1889年10月的《数学学报》上发表，但正如我们将看到的，一个令人震惊的进展介入了。

5.3 塞翁失马，焉知非福

年轻的数学家弗拉格门被赋予为《数学学报》编辑庞加莱回忆录的任务。很快，在1889年夏天，他在回忆录的一部分中发现了对他来说不清楚的陈述和结论。米塔-列夫勒没有意识到其中一点的严重性，并要求进一步澄清。这让庞加莱重新审视了他的工作，他开始对某些收敛性论证产生怀疑。经过几个月的痛苦挣扎，他在1889年12月写信给米塔-列夫勒 [Poincaré 2012]（译文 [Barrow-Green 1997]），称必须进行实质性的修改：

我今天早上写信给弗拉格门，告诉他我犯了一个错误，毫无疑问他已经把我的信给你看了。但这个错误的后果比我最初想象的要严重。渐近曲面 (asymptotic surfaces) 并非封闭的，至少不是我最初设想的那种意义上的封闭。真实情况是，如果考虑这个曲面的两侧（我仍然相信它们是相互连接的），它们会沿着无限多条渐近轨迹 (asymptotic trajectories) 相交（而且，它们的距离变得比 $μ^{p}$ 更高阶的无穷小，无论 $p$ 的阶数有多大）。

我曾认为所有这些渐近曲面，在偏离代表周期解的闭合曲线后，会渐近地趋近于同一条闭合曲线。真实情况是，有无穷多个曲面享有此性质。

我不会向你隐瞒这一发现给我带来的痛苦。首先，我不知道你是否还会认为剩下的结果，即周期解的存在性、渐近解、特征指数 (characteristic exponents) 理论、单值积分 (single-valued integrals) 的不存在性以及林德斯泰特级数 (Lindstedt's series) 的发散性，还配得上你授予它们的伟大奖项。

当时看似灾难的事情，结果却使最终版本的获奖回忆录更加重要。突然之间，它成为了第一篇触及动力系统非可积性 (nonintegrability) 和混沌 (chaos) 主题的论文。然而，它远远领先于时代，直到1960年左右，许多科学家才意识到这项工作的重要性。庞加莱关于“有无穷多个[渐近曲面]享有此性质”的评论预示了更普遍的KAM定理 (KAM theorem)，该定理于1960年左右由柯尔莫哥洛夫 (Kolmogorov)、阿诺尔德 (Arnold) 和莫泽 (Moser) 阐述并证明。应该强调的是，在试图回答弗拉格门的过程中，庞加莱自己发现了错误，并且除了错误的部分，回忆录包含了许多基础性和优美的结果，本身就足以让他多次获得该奖项。

与此同时，米塔-列夫勒承担了避免丑闻和处理已出现实际问题的责任。他是一位熟练的操作者，但这个案例并不容易，因为包括克罗内克、吉尔登 (Gyldén)、林德斯泰特 (Lindstedt) 和委员会其他成员在内的几位科学家对奖项回忆录非常感兴趣，并且持非常批判的态度。国王和公众不会被告知。

包含庞加莱和阿佩尔回忆录的《学报》出版物已经印刷完毕，但除了大约二十份外尚未分发。米塔-列夫勒以几个借口要求退回预发本。新版本必须重新印刷，耗资3500克朗，对于一次印刷来说是一笔巨款。庞加莱被要求支付费用，他毫无异议地照办了。请注意，当时瑞典教授的年薪约为7000克朗，而奖金是2500克朗。另外两位委员会成员被逐步告知情况，这对他们来说是痛苦的，因为他们已经批准了第一个版本。最初提出竞赛问题一的魏尔斯特拉斯尤其感到难过。

就这样，通过米塔-列夫勒的谨慎处理，一场丑闻得以避免。几乎所有印刷的第一版回忆录都被销毁了，而

图5.4 亨利·庞加莱，1889年，35岁，赢得瑞典国王奥斯卡二世颁发的奖项时

米塔-列夫勒尽可能地将有关此事的信息保密。当回忆录 [Poincaré 1890b] 最终于1890年发表时，很少有科学家理解庞加莱的意图。像雨果·吉尔登 (Hugo Gyldén) (1841–1896) 和安德斯·林德斯泰特 (Anders Lindstedt) (1854–1939) 这样的天文学家提出了一些批评意见，但这些相对容易反驳，因为他们使用的级数展开虽然巧妙，但完全是形式化的，即没有证明其有效性。而且，它们没有触及庞加莱描述的复杂动力学。最早掌握庞加莱成果重要性的科学家之一似乎是一位年轻的德国数学家赫尔曼·闵可夫斯基 (Hermann Minkowski) (1864–1909)。

5.4 获奖回忆录

获奖回忆录 [Poincaré 1890b] 中的大部分材料都包含在三卷本的《天体力学》(Mécanique Céleste) 中并有所扩展，因此我们将此讨论留到第9.3节。我们将在这里讨论回忆录第一版中的错误部分，它展示了一种非常自然的思维路线，此后被许多不了解此事已以非常普遍的方式解决的科学家重复了多次。一种宽松的表述是，一般来说，非线性保守系统是不可积的，除了孤立的情况。具有误导性的是，一些现实模型，例如引力二体问题 (gravitational two-body problem)，是可积的 (integrable)。这导致科学家们相信，用包含初等函数 (elementary functions) 或特殊函数的积分来求解微分方程只是一个技巧和勤奋的问题。他们尚未意识到这种解可能存在根本性的障碍。

如前所述，一个著名的可积性例子是引力二体问题，其所有解都可以很好地分类为位于完全填充相空间 (phase space) 的光滑流形 (smooth manifolds) 上的椭圆 (ellipses)、双曲线 (hyperbolas) 或抛物线 (parabolas)。有了这些知识，很自然地期望对问题进行小的扩展，例如增加第三个小质量，可以用类似的方式处理。这就是庞加莱在获奖回忆录第一版中采取的思维路线，该回忆录旨在解决描述 $n$ 个天体在其相互引力场中运动的位置问题。庞加莱考虑了 $n = 3$ 的情况，但通过假设三个质量中的两个是显著的，而第三个质量小到不影响其他两个的运动，进一步简化了问题。这被称为限制性三体问题 (restricted three-body problem)。这意味着对于两个较大的天体，我们可以使用二体问题的解，然后我们尝试描述质量可忽略的天体在两个较大天体引力场中的运动。这种情况模拟了，例如，航天器 (spacecraft) 或小行星 (asteroid) 在太阳和像木星 (Jupiter) 或地球 (Earth) 这样的行星场中的运动。值得注意的是，即使是这个限制性三体问题，至今仍可被认为是完全未解决的。因为尽管已经找到了大量的特殊解，尽管我们可以为给定的初始条件获得特殊的数值解，但我们对6维相空间中轨道行为没有普遍的了解。

庞加莱通过假设三个质量在物理空间的平面内运动，进一步限制了限制性三体系统；这被称为平面限制性三体问题 (planar restricted three-body problem)。在他贡献的一部分中，他进一步简化了模型：两个较大的质量以圆形轨道 (circular orbits) 运动；这被称为平面圆形限制性三体问题 (planar, circular, restricted three-body problem)。这导致了一个具有两个自由度 (degrees of freedom) 的问题，由四个具有周期系数 (periodic coefficients) 的一阶微分方程描述。应该指出，庞加莱在回忆录中为这个问题开发的方法非常有创新性，并且可以用于天体力学之外的更一般问题以及任意维度。

庞加莱考虑的具有四个一阶微分方程的问题包含平衡解 (equilibrium solutions) 和周期解。如果它们是不稳定的，一些解将被吸引到（比如说）一个周期解，而另一些则会被排斥。被吸引解的集合形成一个流形（稳定流形 stable manifold），被排斥解的集合也形成一个流形（不稳定流形 unstable manifold）；庞加莱称这些流形为“渐近曲面”。对于这些曲面上的解，他使用了收敛级数展开，通过这种方式，他可以随着时间的增加跟踪不稳定流形如何偏离周期解，并通过考虑负时间来跟踪稳定流形。他最初的错误假设是稳定流形和不稳定流形的延拓会导致两者光滑地粘合在一起，从而产生一个单一的流形。今天，这被称为同宿流形 (homoclinic manifold)；庞加莱后来在他的天体力学著作 [Poincaré 1892] 中使用了这个术语，以及术语“渐近曲面”。如果存在一个填充相空间的此类同宿流形族（回忆录术语中的渐近曲面），则对应于动力系统存在一个积分不变量 (integral invariant)。

只有在弗拉格门的询问之后，庞加莱才发现这种光滑粘合通常是不可能的，这意味着他的简化三体问题不存在另一个积分不变量。他还意识到，对于这个问题，稳定流形和不稳定流形的相交发生在比代数尺度更小的尺度上。这意味着，在存在小参数 $μ$ （例如，缩放其中一个质量）的情况下，稳定流形和不稳定流形的横截角 (transversality angle) 对于任意大的 $n$ 都小于 $μ^{n}$ 。证明这个结果需要非凡的技术技巧，我们现在知道它对于具有两个自由度的一般哈密顿系统 (Hamiltonian systems) 是有效的。同时，稳定流形和不稳定流形的相交开启了不规则动力学，即我们称之为“混沌”的可能性。应该提到的是，这些不可积性结果适用于比庞加莱考虑的模型更复杂的模型，并且对于更高维度，这些结果变得普遍甚至更加突出。

对随之而来的混沌动力学的一种富有远见且远远领先于时代的描述可以在 [Poincaré 1892, Vol. 3] 的最后一章中找到；亦见本书第9.3节。

第六章哲学与随笔

地质历史告诉我们，生命不过是两次死亡永恒之间的一个短暂插曲，而且即使在这个插曲中，有意识的思维过去没有、将来也不会持续超过片刻。思维不过是漫漫长夜中的一道光芒。但这道光芒才是最重要的。 ——亨利·庞加莱，《科学的价值》

亨利·庞加莱 (Henri Poincaré) 的一些随笔通常被归类为“哲学性的”。其中大部分已收录在六本书中。前五本书没有提及原始论文的出处，这些论文发表在各种期刊上，如《形而上学与道德评论》(Revue de Métaphysique et de Morale)，通常带有数学细节和参考文献，而在书籍版本中则被省略了。省略来源使得这些书能够被广大公众所接受，可能也有营销方面的考虑，因为缺乏来源暗示了这些著作具有更大的原创性。最后一本文集，《科学机会主义》(Scientific Opportunism)，于2002年出版，通过包含来源列表和对截至1913年出版的五本书（由欧内斯特·弗拉马里翁 Ernest Flammarion 出版，其兄弟卡米伊 Camille Flammarion 是一位业余天文学家和多产的科普作家）背景的描述，弥补了这一疏漏。卡米伊·弗拉马里翁撰写了31本科普书籍，均由弗拉马里翁出版社 (Flammarion) 出版。然而，弗拉马里翁兄弟并非科学圈内人士，因此欧内斯特·弗拉马里翁很高兴地接受了古斯塔夫·勒邦 (Gustave Le Bon) (1841–1931)（见图6.1）建立“科学哲学文库”(Bibliothèque de Philosophie Scientifique) 的提议。勒邦并非专业科学家，但他是一位知识渊博、人脉广泛的知识分子。“科学哲学文库”包含了下文列表中的第1、2、3、5项，为弗拉马里翁和勒邦都带来了财富。这六本随笔集及其出版日期如下列表所示：

《科学与假说》(La Science et l’Hypothèse) (1902) [Poincaré 1902]
《科学的价值》(La Valeur de la Science) (1905) [Poincaré 1905b]
《科学与方法》(Science et Méthode) (1908) [Poincaré 1908a]
《学者与作家》(Savants et Écrivains) (1910) [Poincaré 1910]
《最后的沉思》(Dernières Pensées) (1913) [Poincaré 1913]
《科学机会主义：文选》(Scientific Opportunism: An Anthology) (2002) [Poincaré 2002]

图6.1 古斯塔夫·勒邦 (1841–1931)，法国知识分子，在科学、心理学和社会学领域人脉广泛；弗拉马里翁出版社 (Éditions Flammarion) 编辑。

该系列的第一本书是庞加莱的《科学与假说》，在前六个月售出5000册，到1914年总共售出21,000册。大约在1900年，庞加莱在科学界已声名鹊起，但在《科学与假说》出版后，他成为了全国名人。《学者与作家》包含关于杰出人物的传记简述和观察；它由弗拉马里翁出版社在该系列之外出版，并不特别成功，也没有再版。

这些著作在多大程度上是哲学性的？勒内·托姆 (René Thom) 似乎认为它们不是，他发现庞加莱过于数学家而不能成为哲学家 [Thom 1987, p. 72]。此外，他缺乏托姆认为标志着伟大哲学家的本体论 (ontological) 观点。考虑到庞加莱主要关注的问题：科学活动的价值和意义，这种观点难以理解。如果哲学的标准是“对科学真理和人类行为的严肃反思”，那么庞加莱的随笔肯定在哲学 (philosophy) 范围内，正如我们将在他关于数学和物理学中约定论 (conventionalism) 的讨论中看到的那样。

哲学家们对庞加莱哲学著作的争议很快就开始了。伯特兰·罗素 (Bertrand Russell) 在他为弗朗西斯·梅特兰 (Francis Maitland) 翻译的《科学与方法》英译本所作的序言中写道 [Russell 1914]：

阅读以下页面的读者不会惊讶地得知，在我看来，[庞加莱] 对数理逻辑 (mathematical logic) 的批评并非其著作中最好的部分。当他意识到这门学科的存在时，他已经年事已高，并且他被某些轻率的倡导者引导，认为它在某种程度上与他在数学发现中那些被他出色描述的快速洞察力闪现相对立。

然而，当庞加莱开始撰写和讲授关于数学推理 (mathematical reasoning) 的内容时，例如在1900年的国际数学家大会上，他只有四十多岁，而当与逻辑学家 (logicians) 的争议开始时，他大约五十岁；见第6.2节。庞加莱就数理逻辑提出的观点在他生前并未解决。

对哲学家，特别是那些持逻辑主义 (logical persuasion) 立场的哲学家来说，一个问题是庞加莱不太符合经典的讨论和问题表述，而他的著作无疑在科学基础 (foundations of science) 的哲学讨论中发挥着作用。他的出发点总是他自己的数学思维和物理事实，这引导他去理论化真理 (truth)。应该记住，二十世纪初是一个宏大逻辑设计和夸大主张的时期。那个时期的数理逻辑纲领 (mathematical-logical program) 很少顾及工作数学家的需求。庞加莱正确地拒绝了将数学简化为逻辑步骤的做法，因为它会剥夺数学的直觉 (“Anschauung” intuition) 活水源头。庞加莱在《科学与方法》中关于逻辑的随笔更像是揭示逻辑主义 (logicism) 纲领弱点的精彩檄文，而非关于该主题的学术论述；逻辑学家们则承担着反驳他观点的重任。

接下来我们将简要描述随笔中一些反复出现的主题。如上所述，书中的随笔取自期刊或书籍中的文章，通常有所修改。大多数公式被删去，以使随笔对普通公众更具吸引力；实际上，有些章节被删去，有些则被添加。来源和修改由洛朗·罗莱 (Laurent Rollet) 在 [Poincaré 2002] 中给出。还应注意，全集 [Poincaré 1916] 在哲学和科普著作方面并非完全完整。文选 [Poincaré 2002] 的价值还在于它描述了亨利·庞加莱、出版商弗拉马里翁以及编辑古斯塔夫·勒邦之间的关系，后者维持着一个广泛的艺术家、科学家和政治家网络。勒邦定期组织晚宴和其他社交聚会，参与者包括亨利和雷蒙·庞加莱 (Raymond Poincaré)、保罗·潘勒韦 (Paul Painlevé)、卡米尔·圣-桑 (Camille Saint-Saëns)、保尔·瓦雷里 (Paul Valéry) 以及许多其他杰出人物。

6.1 最后的文集：科学机会主义

文选《科学机会主义》[Poincaré 2002] 的历史非同寻常。一位年轻教师路易·鲁吉耶 (Louis Rougier) 找到古斯塔夫·勒邦，提议在他去世后出版庞加莱哲学随笔的第五卷。勒邦对此感兴趣，大约在1919年，他写信给庞加莱的遗孀路易丝 (Louise)，请求允许出版这本新书。她的连襟埃米尔·布特鲁 (Émile Boutroux) 和他的儿子皮埃尔 (Pierre) 已经考虑过这个项目，她被告知他们表示同意。书名将是《科学机会主义》(L’opportunisme scientifique)。

路易丝·庞加莱犹豫不决，因为她的连襟只对该项目进行了粗略考虑，或许也因为她怀疑勒邦和出版商的商业利益。她征求了长女让娜 (Jeanne) 和女婿莱昂·多姆 (Léon Daum) 的意见；多姆是一位杰出的工程师，也是我们今天所说的行业领袖 (captain of industry)。在查看了材料后，多姆得出结论，拟议的文章集没有包含新思想，只有对旧作的小补充和变体。他提议将其中一些文章收录到《最后的沉思》[Poincaré 1913] 的新版中，这在1926年的版本中得以实现，该版本增加了四篇文章。

目前的文选 [Poincaré 2002] 收录了鲁吉耶最初提议的文章。它们涉及几何学基础、天体力学以及科学中的其他各种主题。1909年为布鲁塞尔大学 (University of Brussels) 所作的一次演讲 [Poincaré 1913, Poincaré 2002] 明确阐述了庞加莱关于科学与宗教 (religion) 关系的观点。这在1900年左右的法国是一个热门话题，当时罗马天主教会 (Roman Catholic Church) 在当时的政治、社会和科学问题上持极其保守的立场。

在指出律师关心的不是寻找真相而是说服法官之后，庞加莱指出排除所有先入为主的观点至关重要。他在 [Poincaré 2002, p. 141] 中写道：

不要从这个意义上理解我想要禁止有宗教信仰的人，特别是罗马天主教徒从事科学。上帝保佑！我不会愚蠢到剥夺人类享受巴斯德 (Pasteur) 服务的地步。有些人进入实验室时会忘记他们的信仰；一旦他们穿上工作服，他们就会大胆面对真理，并且像其他人一样具有批判精神。

这表明那些既有宗教信仰又是优秀科学家的人设法同时生活在两个分离的世界中。这一观察符合庞加莱的朋友保罗·阿佩尔 (Paul Appell) 的观点 [Appell 1925a, p. 79]，可以这样表述：

宗教真理在地球上随纬度和经度而变化，但科学是统一的。宗教是个体良知的事情；科学真理对宇宙中所有有意识的存在都是相同的。科学通过小的连续近似取得进步；它永远不会展示万物的最终真理。

对寻求科学真理构成危险的不仅仅是宗教中的教条式思维 (dogmatic thinking)。根据庞加莱在 [Poincaré 2002, p. 141] 中的观点，任何教条主义都会阻碍科学发展：

建立在启示 (revelation) 基础上的宗教教条并非唯一需要担心的。天主教对西方灵魂的影响如此之深，以至于许多最近解放了的精神有一种对依赖的怀旧需求，并一直在努力重建教堂。就这样，某些实证主义 (positivism) 学派只不过是没有上帝的天主教。奥古斯特·孔德 (Auguste Comte) 本人就梦想着规训思想，而他的一些夸大了导师思想的弟子在获得优势后很快就变成了科学的敌人。所有外部束缚都不过是思想的障碍，在接受新的束缚的同时粉碎旧的束缚是不值得的。

在他的著作中，庞加莱主要感兴趣的是获得对物理实在 (physical reality) 和数学实在 (mathematical reality)——两个不同的事物——的洞察。这不应被视为一个过于限制性的纲领，因为它也涉及对心智如何运作、数学应如何教授以及伟大科学家如何发展他们思想的广泛反思。他的写作风格是优美的古典法语，清晰透彻，直指问题核心。他的著作具有一种源自数学和物理学创造性思维实际经验的新鲜感，这是大多数哲学家所缺乏的。可以理解，一位能够写得如此出色的杰出科学家会在公共话语 (public discourse) 中扮演重要角色。

亨利·庞加莱的哲学随笔远非系统性反思的尝试。它们可以被视为对各种形式科学活动的批判性评估。撇开对科学家的描述 [Poincaré 1910]，人们可以在文集中区分出某些反复出现的主题。关于数学和自然科学基础的随笔，关键词是约定 (convention)、假说 (hypothesis)、客观性 (objectivity) 和直觉 (intuition)。然而，在不同的学科中，这些概念可能有不同的含义。

6.2 几何学基础与数学思维

数学基础 (mathematical foundations) 和推理模式 (modes of reasoning) 的主题可以在庞加莱所有的哲学著作中找到。原始随笔写于希尔伯特 (Hilbert) 的《几何学基础》(Grundlagen der Geometrie) [Hilbert 1899] 出现前后。两位伟大数学家之间的对比主要在于希尔伯特的公理化方法 (axiomatic approach) 和庞加莱更偏直觉主义 (intuitionistic) 的思维；关于这些问题的讨论，见 [Eymar 1996, Sanzo 1996, Heinzmann 2010]。

一个基本的概念是，数学中对象的存在 (existence) 与物质对象的存在是非常不同的。像点或三角形这样的数学实体 (mathematical entity)，如果其定义本身或在先前接受的定理范围内不隐含矛盾，那么它就存在 [Poincaré 1902, p. 59]；亦见 [Poincaré 1908a]。因此，庞加莱大胆地将存在等同于无矛盾性 (noncontradiction)。令人惊讶的是，庞加莱在这一点上与逻辑主义者和希尔伯特是一致的。这是法国前直觉主义 (preintuitionism) 与后来以 L. E. J. 布劳威尔 (L. E. J. Brouwer) 为代表的直觉主义 (intuitionism) 不同的主要观点之一。

数学对象理论的发展需要公理 (axioms)，包括明确阐述的和隐含使用的。然而，在数学中，人们可以自由选择这些公理。例如，欧几里得几何 (Euclidean geometry) 基于一个一致的公理系统，但在十九世纪，罗巴切夫斯基 (Lobachevsky)、波利亚伊 (Bolyai) 和黎曼 (Riemann) 表明，通过选择另一个公理系统，可以发展出同样一致的非欧几里得几何 (non-Euclidean geometries)。罗巴切夫斯基通过仅放弃欧几里得公理中的一条，即臭名昭著的“第五公设” (fifth postulate)，实现了这一点：给定一条直线外一点，可以且仅可以作一条直线通过该点与已知直线平行。

数学家选择的公理（或假设）被庞加莱称为“约定”(conventions)。人们可以放弃一个约定而采用另一个，前提是证明相应的几何学，或更普遍地说，相应的数学理论不包含矛盾，也就是说，在数学意义上是一致的 (consistent)。这种数学观被称为约定论 (conventionalism)。

图6.2 路易·库图拉 (Louis Couturat) (1868–1914)，数理逻辑学家，其关于数学基础的观点与庞加莱不同。

请注意，这些观察涉及的是像空间 (space) 和维数 (dimension) 这样的数学概念。正如我们将看到的，约定和约定论在自然科学中扮演着非常不同的角色。与其谈论自然科学的约定，不如为了避免与数学中的约定论混淆而称之为“方便的假设”(convenient hypotheses)。无论是在数学还是在自然科学中，“真理”都是我们所寻求的，但在数学中，根据庞加莱的观点，“真理”是由约定决定的。我们只有在给定的约定体系内才拥有陈述和理论的客观数学真理 (objective mathematical truth)。

庞加莱与法国逻辑学家路易·库图拉 (Louis Couturat) (1868–1914)（见图6.2）之间就逻辑在数学理论中的重要性进行了一场激烈、有时甚至是猛烈的讨论。自十九世纪末以来，包括皮亚诺 (Peano)、弗雷格 (Frege) 和希尔伯特在内的杰出数学家一直致力于通过在一组公理和一套逻辑演绎规则的基础上构建数学来解决数学基础问题。

在这种公理化背景下建立数学应该会产生一致的、没有矛盾的数学理论。庞加莱不同意这种说法，并在 [Poincaré 1908a, Poincaré 1902, Poincaré 1913] 中强调“直觉”是数学思维的一个基本要素。例如，他指出，数学归纳法 (mathematical induction)，这个在数学中经常使用的工具之一，不能仅靠逻辑来证明；它需要直觉。数学家总是想从特殊例子走向更普遍的陈述。他们想展示特殊特征是如何成为更普遍特征的一部分的。那么怎么能称数学是演绎的呢？[Poincaré 1902, 第一章]。庞加莱的论点当然有道理，它们激发了人们对数学与逻辑关系的思考，尤其是在法国以外。不幸的是，在法国，庞加莱的权威导致了对数理逻辑作用的重要讨论的延迟。

数学归纳法

数学推理的基本工具之一被称为归纳证明 (proof by induction)。我们用一个简单的例子来说明。假设我们考虑正整数 $1, 2, 3, \dots, n, \dots$ ，其中 $n$ 代表任意正整数。我们想按顺序将这些数加到某一点。例如， $1 + 2 = 3$ 代表前两个正整数的和， $1 + 2 + 3 = 6$ 是前三个正整数的和，依此类推。让我们用符号 $S_{n}$ 表示加到第n个数的和，因此 $n$ 表示求和的最后一个数。所以 $S_{2} = 1 + 2 = 3$ ， $S_{3} = 1 + 2 + 3 = 6$ ，等等。对于一个大的数 $n$ 进行这种求和是一项繁重的工作，但幸运的是，数学家们为此和推导出了一个公式：对于任何正整数 $n$ ，我们有

S_{n} = \frac{1}{2} n (n + 1) .

我们如何证明这个公式是正确的？对于 $n = 2$ 它显然是正确的，从公式 $\begin{matrix} S_{2} = \frac{1}{2} 2 (2 + 1) = 3 \end{matrix}$ 很容易验证。同样，我们也可以验证它对 $n = 3$ 是正确的。数学归纳法现在将给我们任意 $n$ 的正确性。假设公式对某个 $n$ 是正确的（对于 $n = 2$ 和 $n = 3$ 是这种情况）。基于这个假设，我们将证明该公式对于 $n + 1$ 也必定是正确的。那么，和 $S_{n + 1}$ 是多少呢？我们有

S_{n + 1} = 1 + 2 + 3 + \dots + n + (n + 1) .

因为我们假设了 $S_{n}$ 的公式是正确的，我们可以写成

S_{n + 1} = [1 + 2 + 3 + \dots + n] + (n + 1) = S_{n} + (n + 1)

然后用 $\frac{1}{2} n (n + 1)$ 替换上式中的 $S_{n}$ ，得到

S_{n + 1} = \frac{1}{2} n (n + 1) + (n + 1) = (n + 1) (\frac{1}{2} n + 1) = \frac{1}{2} (n + 1) (n + 2) .

因此，在假设公式对 $n$ 成立的前提下，它对 $n + 1$ 也成立。我们得出结论，该公式对任意 $n$ 都成立。

数学归纳法对于关于正整数的任意陈述都以同样的方式工作。假设我们希望证明一个依赖于正整数 $1, 2, 3, \dots, n, \dots$ 的命题 (proposition)。我们确定该命题对某个 $n$ 值是正确的，例如 $n = 1$ 或 $n = 2$ 。然后我们假设该命题对任意 $n$ 是正确的，并证明由此假设可以推出该命题对 $n + 1$ 也是正确的。由于我们测试了 $n = 1$ 或 $n = 2$ 时的正确性，因此该命题对于 $n = 3$ 必定是正确的，因此对于 $n = 4$ 也必定是正确的，依此类推。也就是说，它对任意 $n$ 都必定是正确的。

关于数学基础和处理逻辑悖论 (paradoxes in logic) 的问题，伯特兰·罗素和亨利·庞加莱都在思考定义 (definitions) 和分类 (classifications) 的恰当特征。关于“分类”，可以想一个集合，其元素通过不同特征被区分或分类；例如，整数集合有偶数和奇数子集。庞加莱称一种分类是直谓的 (predicative) [Poincaré 1913]，如果该分类不因新元素的引入而改变。例如，我们可以将前一百个整数的集合分类为一个小于或等于10的数字子集和一个大于10的数字子集。现在考虑前两百个整数的集合，它当然包含第一个集合。在考虑这个更大的集合时，前一百个整数的分类没有改变，因此该分类是直谓的。非直谓的分类 (nonpredicative classification) 在添加新元素时会改变集合中元素的分类。定义实际上就是一种分类，所以我们要求定义是直谓的。

[Poincaré 1908a] 中一篇著名的文章关注数学发明（或发现 mathematical invention (or discovery)）。庞加莱给这篇随笔取的标题是“数学的发明”(L’invention mathématique)。法语中的 "invention" 一词可以意为发明、发现或找到。英语也存在这种歧义，但更强调新发明的东西。在这篇随笔的英译本中，通常选择“发现”(discovery)，暗示所有数学都具有柏拉图式 (Platonic) 的存在，等待被发现。另一方面，法国数学家雅克·阿达马 (Jacques Hadamard) (1865–1963) 对此主题产生了兴趣，并写了一篇题为“数学领域发明心理学随笔”(Essay sur la psychologie de l’invention dans le domaine mathématique) 的随笔。阿达马监督了他自己著作的英译本，该译本使用了“发明”(invention) 而非“发现”[Hadamard 1990]，这是一个重要的区别。是否有可能监督庞加莱随笔英译本的数学家们不相信数学的一部分是发明？

在一篇精彩的内省 (introspection) 文章中，庞加莱在随笔中描述了顿悟 (sudden insight) 如何在他解决数学问题时降临。他推测，潜意识 (unconscious mind) 在受到意识 (conscious mind) 对问题进行的紧张但看似徒劳的探索刺激后，会考虑许多数学组合，并根据美学 (aesthetics) 或经济性 (economy) 做出选择。他给出的一个发生这种情况的例子涉及福克斯函数。本书第3.3节对此进行了描述。在 [Hadamard 1990] 中，阿达马扩展了这些思想。必须得出结论，“发现”一词的使用与庞加莱关于约定在数学中作用的观点相矛盾。如果考虑数学中的一个基本问题，某个数学结构是在一个更接近于发明的过程中被选定的。经过长时间的思考，灵光一闪给出了正确的方法甚至解决方案。

值得注意的是，对这些思想的一种确认是在阿梅代·曼海姆 (Amédée Mannheim) [Mannheim 1909] 去世后才出现的。1902年，一份研究数学教学的期刊《数学教育》(L’Enseignement mathématique) 询问读者他们是如何发展数学的，思想是如何产生的。在巴黎综合理工学院教授几何学的曼海姆上校就这些问题写下了一些笔记，但他没有寄给该期刊，因为“他不想在公开场合谈论自己”[Mannheim 1909]。他的笔记在他去世后发表在 [Mannheim 1909] 中，提到做数学没有唯一的方法，对他来说，当他在散步、坐在嘈杂的公共马车上或听音乐会时，那是“自行进行”的事情。数学发明对他来说来自他大脑近乎无意识的活动，肯定不是当他坐在办公桌前特别努力的时候。

关于数学中的直觉和逻辑，[Poincaré 1905b] 中有一篇非常有趣的随笔，“数学中的直觉与逻辑”(L’intuition et la logique en mathématiques)。人们可以区分数学家，有些人主要受逐步逻辑引导，有些人则受直觉引导，这是两种不同的风格。也可以区分分析学家 (analysts) 和几何学家 (geometers)，但决定数学风格的不是数学内容。例如，费利克斯·克莱因以非常直观的方式讨论复函数论中的几何问题，但暗示其处理是严谨的。另一方面，魏尔斯特拉斯在发展分析时从不画图或参考图形；他是典型的逻辑学家。黎曼在发展他的数学时不画图，却能唤起直观的几何意象，这对于理解他的思路是必要的。

直觉非常重要，但在大多数情况下它不提供确定性。例如，根据直觉，一条曲线在大多数点上应该有切线 (tangent)，但我们知道存在处处不可微 (nowhere differentiable) 的曲线；因此它们没有切线。所以我们从直觉开始，然后加入推理使证明严谨，这个过程在科学史的进程中得到了提炼和改进。然而，存在不同种类的直觉。一种是基于形式和想象力 (imagination) 的，例如我们关于曲线和切线的（错误的）直觉。这种直觉适合作为起点，但应随后进行严谨的处理。数学归纳法需要另一种类型的直觉；根据庞加莱的观点，它不能通过逻辑步骤来验证，而是通过直觉来证明。归纳证明当然可以被认为是严谨的。

逻辑和直觉在数学中各自扮演着必要的角色。逻辑是证明的工具，而直觉是发明的工具。

[Poincaré 1902] 中有关于“经验与几何”(experience and geometry) 的随笔，[Poincaré 1902, Poincaré 1908a] 中有关于“概率”(probability) 的随笔。关于概率，需要另一种类型的数学约定。

数学中的直觉主义通过 L. E. J. 布劳威尔的思想变得重要起来。强调数学思维中的直觉并不使庞加莱成为这些思想的先驱，但他肯定影响了布劳威尔。关于数学基础的讨论，在直觉主义者和偏爱公理化处理的人之间，在庞加莱去世后变得更加激烈。数理逻辑也提出了一些重要的新元素，揭示了公理化方法中的基本问题；亦见 [Heinzmann 2010]，以及关于历史讨论的有趣记述，见 [Van Dalen 1999]。

6.3 关于数学与数学家

为罗马第四届国际数学家大会（1908年）所作的演讲“数学的未来”(The future of mathematics)，部分转载于 [Poincaré 1908a]，从未像希尔伯特在1900年类似场合提出的23个问题那样受到同样的关注。困难的明确问题或许对数学家特别有吸引力，他们通常比大多数人想象的更务实。但庞加莱的演讲吸引了一些年轻数学家。L. E. J. 布劳威尔 (1881–1966) 于1907年完成论文，参加了这次大会，并写信给他的论文导师 D. J. 科特韦赫 (D. J. Korteweg) [Brouwer 1908]：

能够提升自己到一个可以产生像庞加莱的演讲“数学的未来”那样观点的境界，其真实性每个人都能体验到并接受作为自己工作的指南，这在我看来是任何数学家的最高理想。

庞加莱的文章没有提出很多问题，而是更具哲学性。他的一个陈述是，还有很多数学有待发展，这是大多数数学家充分意识到的，但对许多人来说这是一个令人惊讶的事实，因为对于非研究前沿的人来说，数学可能看起来像一个完成的知识体系。然而，他补充说，研究必须有方向，一种经济感，使我们能够取得更大的进步。其中一个陷阱可能是对精确性的要求，产生过长而乏味的论文；在这里，也需要在不降低精确性的前提下讲求经济。这种观点的一个好例子是引入群 (groups) 和同构 (isomorphisms)，这极大地帮助识别了数学理论中相似但看起来非常不同的部分。

另一点是我们对待来自物理学和工程学问题的态度。当数学家被要求解决某个方程时，他可能会回答说只有少数方程可以解决，而这个不在此列。然而，数学家应该做的是，定性地概述解的行为和特征，然后求助于近似方法 (approximation methods)。在庞加莱时代，这些是级数展开 (series expansions)，我们现在加上了数值技术 (numerical techniques)。事实上，今天的应用数学家正在遵循庞加莱的建议。

最后，讨论了一些代数、拓扑学（位相分析 analysis situs）和数学基础中更具体的问题。研究方向的讨论也在 [Poincaré 1908a] 的随笔“事实的选择”(The selection of facts) 中有所涉及。无论是在数学还是在自然科学中，事实的数量都是无限的。我们如何选择事实以富有成效地发展科学？事实存在等级，有趣的是那些可以被多次注意到和使用的。它们不应该是偶然的。

在 [Poincaré 1913] 中，我们在“为什么空间有三维”(Pourquoi l’espace a trois dimensions) 一章中找到了关于拓扑学，“位相分析”的讨论。除了处理距离和坐标的度量几何学 (metric geometry)，以及处理几何对象可能变换和映射的射影几何学 (projective geometry)，我们还有第三种可能性，即位相分析，或称“橡皮几何学”(rubber geometry)；我们将在第十章更详细地回到这个主题。

有趣的是，庞加莱认为位相分析是一个直觉作用非常明显的学科。一个原因是三维空间的经验指导了我们的基本定义和命题，而当考虑超过三维的几何时，这种经验变得更加重要。

这部分几何学关注的是在允许连续变形 (continuous deformation) 时图形的等价性 (equivalence)。因此，一个圆等价于一个椭圆，实际上等价于任何闭合曲线，因为我们可以将这样的曲线连续变形为一个圆；三维空间中的一个球面等价于一个椭球体和一个立方体，等等。但一个球面不等价于一个环面 (torus)，因为环面上的孔阻止了其向球面的连续变形。

今天，像维数这样的拓扑概念不会被认为是哲学性的。然而，在庞加莱的时代，情况确实如此。例如，在维数的处理成为拓扑学的一部分之前，哲学家和科学家们用混合了数学、物理和哲学术语的方式来讨论它。

6.4 自然科学原理

自然科学有两个基本要素：来自实验 (experiment) 和观察 (observation) 的经验 (experience)，以及推广 (generalization)。在描述我们如何基于这些基本要素找到真理之前，我们讨论两个例子。

考虑一个简单的实验：我们拿一个小铁球让它落到地上。我们可以重复实验并记录下落时间、球的重量和其他实验参数。我们从相似的实验中不会得到完全相同的结果，但它们会非常接近，我们可以提出一个关于引力 (gravitational force) 的假说，它是球落地的原因。小的实验偏差似乎并不困扰我们，我们只能进行有限次数的实验来预测未来无限多种下落物体的类似事件这一事实也不困扰我们。此外，我们可以进行其他相关的实验，例如用摆动的摆锤，并期望关于引力的相同假说将帮助我们解释和预测摆的运动。我们所描述的是实验与推广的相互作用。

现在我们考虑一个复杂得多的现象，我们不是从实验开始，而是从一个假说开始：地球围绕太阳公转并绕其轴自转。更准确地说，我们断言地球沿着一个近乎圆形的轨道围绕太阳运行，每年公转一周，同时每天绕其轴自转。我们描述的是一个复杂的运动，这是一个一世纪的数学家兼天文学家托勒密 (Ptolemy) 会不同意的假说。他的观点是地球静止在宇宙中心，所有天体都围绕它以圆形轨道运动。现代观点有充分的论据支持：(1) 它不仅得到验证地球和天体位置如我们假说预测的观测支持，也得到我们假定的动力学定律的支持。(2) 地球在两极的扁平可以解释为轴向自转的结果。(3) 傅科摆 (Foucault pendulum) 的行为方式支持自转假说。(4) 地球上的大尺度风循环可以用其自转来解释。(5) 像气旋 (cyclones) 和龙卷风 (tornadoes) 这样的涡旋运动表现出支持地球自转的朝向。还有许多其他的论据。在现代科学的背景下，地球自转是一个方便的假设，与托勒密的观点形成对比，后者在两千年前可能是方便的，但不再符合科学标准。

请注意，术语“方便的”不同于数学中的“约定”。不幸的是，庞加莱混淆地将术语“约定”同时用于数学和自然科学。本质区别在于，自然科学中的假说不是任意的；它们基于经验。我们更详细地考虑这个主题，遵循 [Poincaré 1902] 和 [Poincaré 1905b]。

在考虑自然科学时，人们意识到由实验和观察组成的经验远非完美，因为我们无法隔离现象。例如，实验者在干扰被观察现象方面扮演着角色，并且总有被忽略的力，例如在落下的铁球案例中，可能的风力和球与空气之间的摩擦力 (friction)。但我们可以说服自己，这些因素只引起小误差，并且在类似情况下会有类似的结果。其次，我们进行一种插值 (interpolation)：我们只能进行有限次数的实验，但我们的结论是关于连续的数据 (continuum of data)。例如，在落球的情况下，我们期望我们的结果适用于连续的重量、球的大小和球被释放的高度。通过这种插值，我们已经进入了第二阶段，即理论化 (theorizing)。

关于经验的理论化涉及第二个要素，推广。这反过来又导致对其他结果的预测 (prediction)，我们再次通过经验来检验。在推广中，我们的基本假设是存在一个相对简单的定律 (law) 来解释经验。例如，我们假设质量之间存在引力，它在整个宇宙中是相同的，并且其作用可以用一个相对简单的数学方程来形式化。考虑到天体运动的复杂性和太阳系中粒子的数量，这个假设是相当了不起的。因此，我们基本上假设的是，我们可以用有限数量的相对简单的定律来解释自然界经验的复杂性，即大量的事实。

科学永远不会完成，科学问题也永远不会完全解决。一个问题总是只在一定程度上和一定近似下得到解决。然而，我们用于发展理论的术语“方便的假设”不应与任意性混淆。尽管科学理论和假说发生了巨大的变化和重新表述，但由于它们源于经验，科学的概念和定律对应着真实的关系 (real relationships)。科学所阐述的自然定律是近似的，随着每一代人在前代人奠定的基础上开始，其质量会随着时间的推移而提高。正如庞加莱可能会说的，定律变得更具或然性 (probable)。例如，能量 (energy) 的概念最初归因于经典力学中的运动。然后发现动能 (kinetic energy) 可以转化为热量 (heat)，后来又发现电场 (electrical fields) 和磁场 (magnetic fields) 包含能量。因此，能量的概念演变了，由此产生的物理定律变得更普遍、更具或然性。

我们说过地球自转是一个方便的假设。这是否意味着人们仍然可以自由地假设托勒密提出的地球是宇宙不动中心的系统？当然不是。在现代科学的背景下，托勒密假说的概率为零。自转假说具有与我们周围可观察物体的存在相同的确定性。对于现代科学来说，托勒密的假说不再方便。

自然科学，与数学相反，首先是一种表征经验和建立物理实在事实之间关系的方式。只有在这些关系中，科学才具有客观性。根据庞加莱的观点，科学并不向我们展示事物的本质、我们处理和观察的对象的本质，而是对象之间的关系。

考虑物理学的一个成熟部分，经典力学 [Poincaré 1902]。有趣的是，英国和欧洲大陆物理学家的风格有所不同。前者认为力学是一门实验科学，而欧洲大陆的物理学家则将经典力学表述为基于先验 (a priori) 假设的演绎科学。庞加莱同意英国的观点，并观察到在欧洲大陆的力学书籍中，从未明确哪些概念来自经验，哪些来自数学推理，哪些来自约定和假说。在欧洲大陆书籍中要么被忽略，要么最多得到模糊处理的问题包括以下几点（亦见 [Poincaré 1905b]）：

不存在绝对空间 (absolute space) 和相应的绝对参考系 (absolute frame of reference)。
不存在绝对时间 (absolute time)。
我们无法测量时间间隔的相等性和不同地点时间的相等性。
欧几里得几何未经讨论就被使用，但这种几何对于经典力学并非必不可少；它仅仅是一个方便的假设。

以惯性定律 (law of inertia) 为例：一个不受力作用的物体以恒定速度沿直线运动。这是否先验地清楚？当然不是。该定律实际上是在相当现代的时期才被阐述的。直线 (straight line) 的概念基于欧几里得几何的方便假设，而力 (force) 或其不存在的概念并非基于经验，而是遵循一个合适的定义。

科学的客观价值

庞加莱将自然科学中的约定表述为方便的假设，这在他那个时代的哲学家中引起了反响。庞加莱在 [Poincaré 1905b] 的两章中详细阐述了这些主题。

在回应数学家兼哲学家爱德华·勒鲁瓦 (Édouard Le Roy) (1870–1954) 时，庞加莱在 [Poincaré 1905b, 第十章] 中问道，科学是否是人为的。勒鲁瓦是亨利·柏格森 (Henri Bergson) 的学生，被认为是唯名论者 (nominalist)。在唯名论 (nominalism) 中，科学被认为是纯粹的约定。这既适用于理论也适用于事实。科学家只整理经验；他使用纯粹形式化的描述语言（术语唯名论源于命名）。在这种观点下，所有对原则绝对真理的信念都完全破灭了。

庞加莱指出，在这种哲学中，不仅事实和理论是科学家的人为构造，而且整个科学事业都高度反智 (anti-intellectual)。在唯名论看来，人类智力 (human intelligence) 和人类语言 (human language) 扭曲了它们所触及的一切。实在 (Reality) 是易变的，在我们把注意力转向它的那一刻就逃脱了我们。其最终结果是对所有智力成就的怀疑主义 (scepticism)。对勒鲁瓦来说，科学由一套规则或定律组成，而不增加真正的知识。然而，正如庞加莱观察到的，这些规则并非任意的。它们解释经验并导致预测，这是任意规则所缺乏的。科学是不完美的，但包含可以使用的知识。

勒鲁瓦哲学的另一个奇怪方面是他关于科学家创造事实 (creates fact) 的概念，或者更具体地说，存在一个裸事实 (bare fact) 和一个被创造出来的科学事实 (scientific fact)。例如，我们可以比较白天变暗这个裸事实和发生日食这个科学事实。根据庞加莱的观点，裸事实和科学事实之间的区别并不总是那么清晰，因为有些事实只能间接验证。在某些时候，区别仅仅在于表达它的语言。科学事实只不过是用另一种语言翻译过来的裸事实，科学家唯一创造的就是描述事实的语言。实际上，情况甚至更复杂，因为科学家通常会结合几个裸事实来表述和翻译成一个科学事实。

庞加莱补充说，在制定定律时，科学家拥有更大的自由度。通过观察某些规律性，科学家们获得了定律，然后，通过无意识的唯名论，得出了诸如牛顿引力定律在宇宙中无处不在这样的原则 (principles)。定律可以永久修订，但对于原则，我们必须调整或简化事实。如果所有定律都变成了原则，科学就不复存在了；这是唯名论的一个基本局限。我们的物理定律随着所选择的约定而改变。那么一个遗留的问题是，在所有这些定律的变化中，是否存在独立于约定而有效的普遍不变量 (universal invariants)。如果能找到这样的普遍性，它们将存在于裸事实之间，而不是科学事实之间，因为科学事实之间的关系总是受约定支配的。

6.5 数学物理笔记

庞加莱的时代也不例外，总是存在着仅仅出于功利目的看待自然科学的倾向，特别是仅根据它们产生经济利润的程度来评价它们。有权势的人希望将科学研究限制在寻求实用发明，以用作工业开发的工具。在 [Poincaré 1905b, 第5章, p. 138] 中，庞加莱为科学研究的自主性 (autonomy) 辩护：

此外，只着眼于应用的科学是不可能的；经过验证的结果只有在相互连接成链条时才富有成果。如果只关注那些期望立即产生结果的部分，连接的组成部分就会缺失，链条也就不复存在了。

数学物理及其组成部分——即数学和物理学——之间的关系在 [Poincaré 1905b] 中得到了广泛讨论。接下来，我们分三部分介绍庞加莱对其中一些主题的看法。分析与物理学之间的关系也是庞加莱在苏黎世第一届国际数学家大会（1897年）上全体报告的主题。

分析与物理学

数学有三个目标：提供研究自然的工具，服务于哲学和美学目的，最后与物理学家密切合作发展。今天，经验是所有物理思考的起点，但要表达物理定律需要语言。只有在数学中才能找到唯一合适的语言。例如，在热力学的发展中，“热”(heat, “chaleur”) 这个词并不令人满意，因为它暗示了一个固定的量，一种物质，而不是一种动态状态。找到描述现象的恰当词语至关重要。经验并不精确，但物理定律是精确的。它们源于推广，问题在于如何从众多可能性中进行选择。是数学精神将其简化为纯粹形式；例如，在数学中人们使用术语“乘法”(multiplication)，但它指代整数、四元数 (quaternions) 和许多其他元素。顺便说一句，四元数是作为抽象数学构造出现的，但物理学家后来发现了它们的用途。这就是数学家为物理学提供的服务，但要履行这项服务，数学家必须在没有即时实用性考虑的情况下工作。数学家必须像艺术家一样工作。

看一些例子是有启发性的。在第一个例子中，我们可以看到语言的改变可能会引发新的推广。在开普勒定律 (Kepler’s laws) 中，人们看到了行星在椭圆轨道上的几何和动力学运动。在向牛顿定律过渡的过程中，人们开始使用微分方程，这使得描述比二体问题复杂得多的引力系统成为可能。

第二个例子涉及麦克斯韦方程组 (Maxwell’s equations)。当麦克斯韦开始探索时，当时的电动力学方程很好地解释了当时的实验。然而，麦克斯韦认识到在方程中增加一个小项会使它们更对称。后来的实验需要这个项来解释新现象。物理学家麦克斯韦之所以有这种观点，是因为他习惯于用对称性、向量 (vectors) 和虚（复）量 (imaginary (complex) quantities) 的语言来思考。

第三个例子展示了数学现象之间的数学类比 (mathematical analogies) 如何帮助我们发现新的物理现象。拉普拉斯方程描述了牛顿引力、流体运动、电势 (electric potentials)、磁势 (magnetic potentials)、热传播和许多其他现象。一个领域的意象激发了对其他领域类似现象的思考。例如，流体动力学 (hydrodynamics) 中的通量 (flux) 概念启发了电动力学 (electrodynamics) 中的类似现象。

反过来，数学从物理学中获得了什么？首先，自然提供了印象并提出了我们必须回答的问题。在数学中，有无限多种对象的组合，那么我们如何选择数学研究的方向呢？物理学帮助我们选择。它还引导我们思考以前没有想象过的问题。没有物理学，我们可能原地打转。无论人类的想象力有多少变化，自然界包含的变化要多得多。

一个简单的例子可以证明这一点。一个自然的数学对象是整数 (whole number, integer)。然而，外部世界迫使我们发明了连续统 (continuum)，这反过来又导致了微积分 (differential calculus)。因此，微积分提供了数论 (number theory) 所缺乏的视角。另一方面，傅里叶理论 (Fourier theory) 最初是为了分析热传播而发明的，但现在也用于表示不连续函数 (discontinuous functions)。如果这个问题不是自然产生的，数学家们会有足够的进取心去研究导致不连续函数的级数吗？

对其他类型级数的需求也源于物理学。此外，偏微分方程理论以其多种形式的发展完全是由物理现象引发的。

另外一点，物理学不仅仅是提出问题。它有助于解决问题。例如，在拉普拉斯方程的情况下，物理现象唤起了几何意象，这反过来又可以用来解决相关问题。最重要的发现是通过猜测在证明之前做出的。但需要注意的是，不存在两种严谨性，一种数学严谨性 (mathematical rigour) 和一种物理严谨性 (physical rigour)。尽管如此，在物理学中有时修改工具会有所帮助。例如，在分析某些函数时，有时可以将自己限制在多项式上。现在有如此多的数学结果，这种修改通常是可能的。

数学物理的历史、当前危机与未来

[Poincaré 1905b, 第7-9章] 中关于数学物理当前和未来的笔记大多具有历史意义。与将物理学定律或原则视为约定（或方便的假设）的讨论一致的是对定律表述变化的观察。早期，比如说直到1600年，物理定律是静态的，表达了宇宙现象的内在和谐。随后的危机修改和改变了那些定律。在此背景下，庞加莱讨论了牛顿定律、带有迈克尔逊-莫雷实验 (Michelson–Morley experiment) 的相对性原理、洛伦兹收缩和局部时间概念、拉瓦锡原理 (principle of Lavoisier)（质量守恒 conservation of mass）、迈耶原理 (principle of Mayer)（能量守恒 conservation of energy）以及卡诺原理 (Carnot principle) 与可逆-不可逆 (reversible–irreversible) 的讨论。

根据庞加莱的观点，新的实验将推翻公认的物理原理，并且预计会出现一种新的力学，例如基于统计学的气体动力学 (dynamics of gases) 力学。

科学与实在

[Poincaré 1905b] 的最后两章关注科学在文明中的性质和作用。所有自然定律都是近似的 (approximative)，但这并不意味着它们是偶然的 (accidental)。自然科学中定律的表述意味着，如果满足某些条件，某些事情可能会发生，而科学的进步意味着所表述的定律在预测给定条件下将发生什么方面将越来越有用。

例如，人们观察到先行事件 $A$ 产生后果 $B$ ，并假设一个接近 $A$ 的先行事件 $A^{'}$ 将产生一个接近 $B$ 的后果 $B^{'}$ 。这个假设显然是 $B$ 连续依赖于 $A$ 。在这种推理中，人们排除了小的影响，尽管影响实验的现象无法完全隔离。此外，人们应用归纳法 (induction)（从具体到一般的推广，不要与上文描述的数学归纳法混淆）。由于自然界中存在许多相似的情况，我们的实验并非独一无二，但它可以以相当好的近似度重复进行。形式为 $A \to B$ 的序列没有一个会完全相同，但许多会近似相似，我们可以尝试对它们进行分类。这实际上是对决定论 (determinism) 的一种选择。

科学中的客观性通过与他人的接触得到保证。这些其他人正在观察相同的事物；我们显然不是在梦中行走。科学客观性的一个条件是经验被许多其他人共享。传播通过话语进行：没有公共讨论，就没有客观性。

另一方面，我们不知道我们是否以相同的方式体验相同的事物。因此，个体体验的感觉 (sensations) 无法传递。但我们可以传递的是感觉、经验之间的关系。客观性仅限于关系。

有人可能会评论说，审美情感 (aesthetic emotion) 对大多数人来说是共同的，但这并不意味着审美感觉是相同的，而是指在这方面与他人有着和谐而富有成果的互动。

因此，科学首先是一种分类，一种处理和整理事实的方法。它是一个关系的系统，而这些事实（或对象）之间的关系可以被认为是客观的。那么可以问两个问题：

科学是否告诉我们事物的真实本质？
科学是否告诉我们事物之间关系的真实本质？

关于第一个问题，庞加莱写道 [Poincaré 1905b, 第11.6节]：

关于第一个问题，没有人会犹豫回答“不”。但我相信可以更进一步：不仅科学不能告诉我们事物的本质，没有任何东西能够告诉我们，而且如果某个神知道它，他也找不到词语来表达它。我们不仅猜不到答案，而且即使有人告诉我们，我们也无法理解它。我甚至怀疑我们是否很好地理解了这个问题。

第二个问题的答案取决于我们的陈述和共识在我们之后是否会持续存在。我们可以坚持认为，尽管理论来来去去，但某些关系在所有变化中幸存下来。有点讽刺的是，庞加莱提到的一个持久概念的例子是电磁波传播理论中的以太。现代物理学不再需要以太的概念。一个更好的例子是地球自转作为一个解释许多现象的假说。它具有与外部对象，如椅子或桌子，相同程度的存在性。从运动学 (kinematically) 上讲，“地球自转”和“地球不自转”的陈述都是正确的。更进一步说，陈述其中一个正确而另一个不正确意味着假设存在绝对空间和坐标。但正如我们之前看到的，在物理学中，“地球自转”的陈述具有更丰富的内容，因为它解释了许多关于不自转假说无法告诉我们任何信息的现象。地球自转是一个方便的假设，通过类似的推理，地球围绕太阳运动也是如此。

最后，必须为了科学而从事科学。了解所有事实是不可能的，所以我们必须选择。科学家选择事实并非着眼于有用的应用；他们选择比其他事实更有趣或更美的事实。

第七章终其一生，他是怎样一个人？

亨利·庞加莱 (Henri Poincaré) 于1912年7月17日逝世。在他生命的最后一年里，他非常活跃，前往参加国际会议并履行许多其他义务。6月26日，即他去世前几周，他发表了第十二章中介绍的关于道德教育 (moral education) 的公开演讲。他在1908年罗马 (Rome) 国际会议上经历的前列腺问题 (prostate problems) 变得更加严重，医生建议他接受手术。7月6日星期六，他参加了一个讨论群论 (group theory) 的教务会议；会后，他告诉朋友保罗·阿佩尔 (Paul Appell)：“明天我就要住院了。”手术于7月9日进行，似乎很成功；家人和朋友们都感到高兴和放心。一周后，一次栓塞 (embolism) 突然终结了他的生命。

庞加莱的意外去世在法国和整个科学界都被视为巨大的损失。保罗·阿佩尔在 [Appell 1925a] 中写道：

庞加莱的一生是紧张而不间断的沉思。它完全奉献给了科学工作和家庭。它将永远是法国青年钦佩的对象和榜样。

在 [Darboux 1913] 中，引用了阿佩尔在庞加莱去世后的评论：

关于问题，他具有天才的天赋，能立即看到，包括特殊细节，其来源的普遍思想及其在整体中的位置。他还具有那种不矫揉造作、那种对效果的反感、那种在洛林 (Lorraine) 常见的常识 (common sense)，那种他一生都保持着的特殊善良天性。

庞加莱憎恶偏见 (prejudice)，例如认为某个政党 (political party) 的一切总是好的、正当的，而另一个政党的一切总是错误的这种假设。他不想在简化的选择之间做出抉择。对他来说，在寻求真理的过程中既没有怀疑主义 (scepticism)，也没有既定的启示。宗教真理在全球各地有所不同，但科学并非多样化；它是一个统一体。宗教是个体良知的事情，而科学真理对每个人，甚至对宇宙中所有有感知能力的存在都是相同的。另一方面，科学通过小的连续近似取得进步。它永远不会达到任何事物的最终真理。

图7.1 庞加莱在家里的书桌前

阿佩尔也谈到了庞加莱的爱国主义 (patriotism)。这对我们来说可能显得过时，但必须认识到，作为一个男孩，亨利目睹了1870–1871年战争的敌对行为，包括阿尔萨斯 (Alsace) 和洛林部分地区割让给德国，这种损失在当时仍然是现实；那些地区直到1918年第一次世界大战后才归还法国。1912年春天，庞加莱写了关于伦理与科学的随笔 [Poincaré 1913]：

当人们要求我们为我们的爱国之情辩护时，我们可能会变得非常尴尬，但想象一下我们战败的军队和被入侵的法国，我们的心会振奋起来，泪水会涌入我们的眼睛，我们将不再倾听。而如果现在某些人散布如此多的诡辩 (sophisms)，那无疑是因为他们缺乏足够的想象力。他们无法想象所有坏事，而如果不幸或来自上天的某种惩罚打开了他们的眼睛，他们的灵魂会像我们一样反抗。

阿佩尔多年担任索邦大学 (Sorbonne) 理学院院长，他回忆说庞加莱对新的学术任命 (academic appointments) 相当感兴趣。他不会自动投票给最年长和最有经验的候选人，而是投票给他认为具有最佳科学素质的人。作为同事，他性情温和，非常认真负责，对自己要求很少。

应米塔-列夫勒 (Mittag-Leffler) 的请求，皮埃尔·布特鲁 (Pierre Boutroux) (1880–1922)——阿琳·庞加莱 (Aline Poincaré) 和埃米尔·布特鲁 (Émile Boutroux) 的儿子，本人也是一位数学家和科学史家 (historian of science)——写下了关于他叔叔的日常生活、习惯和性格的文章；该文转载于 [Boutroux 1921]。根据布特鲁的说法，他叔叔思想的活跃就是他在家工作（见图7.1）、在家人中间、或在他避暑别墅花园里工作时所需要的全部。工作时，他通常毫不犹豫地书写，偶尔只做少量修改。一篇新文章完成后不久，庞加莱就对其失去了兴趣，几乎不看印刷厂寄来的校样 (proofs)。但那是显而易见的工作时段。不太明显的是他总是在工作：在教学楼之间行走时，下午在户外散步时，参加研究所 (Institute) 会议时，甚至在沙龙 (salons) 的社交场合，他有时会突然打断谈话去追随自己的思绪。

关于与学生和同事的互动，值得注意的是，在进行新研究时，他不太相信讨论和思想交流。也许这对他来说太慢了，而且他也将研究视为个人的奋斗，一场没有见证人的对抗。研究对他来说是一件非常私人的事情。这在某种程度上解释了为什么他学生很少。他与学生的接触主要通过他的许多讲座进行。在他为数不多的研究学生中，我们前面提到了路易·巴什利耶 (Louis Bachelier)、迪米特里·蓬佩乌 (Dimitrie Pompeiu) 和米哈伊洛·彼得罗维奇 (Mihailo Petrović)。大约在1900年，教授和学生之间没有太多个人接触，但即使在那个时候，这种几乎完全缺乏沟通的情况也是不寻常的。布特鲁回忆起，在一次访问哥廷根 (Göttingen) 期间，他被那里数学家们活跃的气氛以及许多正式和非正式的讨论所震撼。尽管如此，庞加莱对初学者非常理解和同情。当他们来访时，他总是乐于倾听。但当涉及到要讨论的结果时，他要求非常高。如果没有真正的新见解，他通常的评论是“À quoi bon?”（这有什么用？）。

他不是科学书籍和文章的狂热读者，如果他阅读，也是以一种特殊的方式。他直接去看结果，然后自己重构推理和论证。他的思维方式非常直接，从问题表述开始，跳过长长的演绎步骤链条到达一个重要结果，然后再检查结果。这也使得与他交谈有时很困难，因为他会突然从一个话题跳到另一个看似无关的话题。这种思维模式与他处理的众多不同科学主题相符。庞加莱对文学 (literature) 和地理学 (geography) 感兴趣。他喜欢旅行，目的是参观著名景点，而不是为了消遣或实现某种浪漫想法。他很少去同一个地方两次；看见和探索新事物是他个性的主导部分。

亨利·庞加莱对文化 (culture) 和科学有着广泛的兴趣。他远非一个狭隘的专家 (specialist)。这种兴趣范围伴随着巨大的责任感 (responsibility)。一次谈话中，有人提到一位数学家离开了他的领域去做完全不同的事情，并补充说这个人可能在他的新职业中感到同样满足，就像他作为科学家时一样。庞加莱表示抗议。布特鲁将此解释为他叔叔的观点，即只要有东西可以探索，就有义务继续下去。研究对庞加莱来说是一种责任 (duty)。他可能对许多事情持讽刺态度，但对科学则不然。（也许所讨论的数学家是潘勒韦 (Painlevé)，他在索邦大学拥有教席，于1906年开始涉足政治，并于1910年离开科学投身政治。）

心理学家爱德华·图卢兹 (Édouard Toulouse) 进行了一项奇特但可能有趣的研究。庞加莱接受了图卢兹对其心理组织 (mental organization) 的分析，后者随后就此写了一本书 [Toulouse 1910]。分析在巴黎心理学实验室 (Psychological Laboratory) 进行，得出了一些不太令人兴奋的观察结果。例如：

他每天在同一时间段工作，时间不长。数学研究每天花四个小时，上午两小时，下午5点到7点两小时。
他通常的工作习惯是先在头脑中解决问题，然后写下来。
他左右手都能写字 (ambidextrous)，并且近视 (near-sighted)。
他能很好地记忆和形象化 (visualize) 他阅读和听到的内容。
他身体笨拙，没有艺术天赋 (artistically gifted)。
他总是很匆忙，讨厌回头修改。
他相信让他的潜意识处理一个问题，同时他有意识地处理另一个问题。

图卢兹也检查了其他杰出且富有创造力的公民，例如左拉 (Zola)、贝特洛 (Berthelot)、罗丹 (Rodin) 和圣-桑 (Saint-Saëns)。

加斯东·达布 (Gaston Darboux) 为亨利·庞加莱宣读了一篇颂词 [Darboux 1913]，发表在全集第二卷中。关于他的工作方式，他指出庞加莱致力于最困难的问题，最好是以最普遍的形式。当他对一个问题有了理解后，他不会回头去润色表述或论证，而是直接转向下一个问题。有趣的是，达布认为庞加莱最辉煌的成果是他在福克斯函数和克莱因函数 (Kleinian functions) 方面的成就，这也反映了1910年左右数学家们的关注焦点。关于为奥斯卡二世国王撰写的获奖回忆录，可以理解他没有提及最后一刻的修改，但他提到了克罗内克对程序的批评。根据达布的说法，这次获奖是庞加莱的名字开始为公众所知的开端。他真正为广大公众所熟知是通过他的哲学著作。那些书是畅销书，并经常被翻译。《科学与假说》在最初十年售出数千册，并被翻译成二十多种语言。

根据达布的说法，庞加莱当然知道他在科学上取得成就的价值，但他从未为自己要求任何特殊的东西。他对请求的反应通常是积极的。例如，当被要求讲授关于他理论的应用时，他欣然同意。当蒂塞兰 (Tisserand) 于1896年去世时，庞加莱正在教授数学物理，但当被要求转而教授蒂塞兰的数学天文学课程时，他毫不犹豫地接受了。

尽管如此，他的主要兴趣仍然是“寻找真理”。他参与了大地测量工作 (geodetic work)、无线通信 (wireless communication) 以及天文台理事会 (council of astronomical observatories) 的监督工作。他履行了这项参与所带来的所有任务，但他对行政管理 (administration) 并不真正感兴趣。

在阅读了亨利·庞加莱同时代人的观点之后，在他去世一百年后的今天，我们能说些什么呢？

他有幸拥有幸福的童年、幸福的婚姻和好朋友。正如那个时代通常的情况一样，他将个人感情和事务限制在家人和密友的圈子里。即使是与米塔-列夫勒的长篇、持续的通信也很少涉及私人事务。

阿佩尔称他性情温和，但他肯定表现出了斗争精神，这在他与费利克斯·克莱因的交流中变得清晰。但这是一种没有恶意、没有持久积怨的斗争精神。

亨利·庞加莱受到好奇心的驱使，去理解自然现象，去发现和阐述数学思想，去理解人类心智的运作方式，并去研究许多其他引起他兴趣的主题。他的创造力造就了异常庞大的科学产出，一份持久的遗产。他是如何变得如此多产的？是什么让他成为天才 (genius)？除了他情感健全和平衡的精神，我们可以注意到三个因素：他高超的智力 (intelligence)，非凡的记忆力 (memory)，以及对科学问题完全和持久的痴迷。他真的从未停止过对科学的思考。

庞加莱在努力发现和解释方面认真负责，但他也缺乏耐心，也许是因为他视野如此开阔，并且急于转向下一个问题。他在讨论笔迹学和他自己的笔迹时提到了这种不耐烦；皮埃尔·布特鲁回忆说庞加莱不太擅长校对他论文的校样。关于他对科学和社会的责任感，他非常认真负责。很自然地，公众将庞加莱与法国的当权派联系在一起。这与他显赫的社会地位以及他与保守派共和国总统雷蒙·庞加莱的家族联系相符。然而，这对他并不公平。亨利·庞加莱直言不讳地谈论偏见的危险，例如在宗教和哲学领域，并且他在德雷福斯事件中采取了非常独立的立场。

关于亨利·庞加莱最引人注目的是他的多才多艺 (versatility) 以及他开创了全新的研究领域，包括：

自守函数 (Automorphic functions)，单值化 (uniformization)
微分方程的定性理论 (qualitative theory of differential equations)
分岔理论 (Bifurcation theory)
渐近展开 (Asymptotic expansions)，范式 (normal forms)
动力系统 (Dynamical systems)，可积性 (integrability)
数学物理 (Mathematical physics)
拓扑学 (Topology)（位相分析 analysis situs）

在许多学科中，庞加莱都领先于他的同事，而这样的人有时会被忽视甚至受到敌视。然而，他领先的地位并未妨碍同事们对他的钦佩以及他与许多不同人的接触。情况本可能不同，但他对把握时代重大问题和人们最关心的问题有着良好的感觉。他巨大的产出当然也有帮助。“自守函数”和“位相分析”不太可能吸引普通公众，但“太阳系的稳定性”、“相对性原理”以及他的哲学随笔则做到了。

他的写作风格使得他的作品易于被来自不同领域的科学家所理解。这与现代数学写作，特别是某些纯粹数学学派的写作形成对比。但正如达布和他那个时代的其他同事所指出的那样，在他自己的时代就已经有人反对庞加莱的风格。正如维托·沃尔泰拉 (Vito Volterra) 所写 [Volterra et al. 1914]：“他在科学家中就像印象派画家 (impressionist) 在艺术家中一样。”他的写作就像一场谈话，他向读者阐述他对一个问题的想法。他在文章中间最常使用的转折语是“ce n’est pas tout”（这还不是全部）。确实，庞加莱常常大步跳跃，需要填补一些重要的细节；他的不耐烦和他急于前进的迫切愿望一直都在显现。但引人入胜、可读性强的风格以及丰富的新思想足以弥补这一切。

科学家们常常处于竞争之中，不断地评价他们的同事并将自己与他们比较。理查德·费曼 (Richard Feynman) 诙谐地称一位科学家为“大人物”(big shot)，另一位为“小人物”(small shot)。与过去150年的科学家相比，庞加莱的地位应该如何评价？一个名字立刻浮现在脑海：大卫·希尔伯特，一位杰出的数学家，尽管他在研究主题的选择上更为局限。然而，两人的风格截然不同，试图比较希尔伯特和庞加莱没有什么意义。亨利·庞加莱自成一派 (in a class by himself)。