压缩感知 (Compressive Sensing) 「讲义」

12 May, 2025

文章来源：CS Notes

Richard Baraniuk，莱斯大学 (Rice University)

[《IEEE Signal Processing Magazine》讲座笔记] 第24卷，2007年7月

1 范围 (Scope)

香农/奈奎斯特采样定理告诉我们，为了在对信号进行均匀采样时不丢失信息，我们的采样频率必须至少是其带宽的两倍。在许多应用中，包括数字图像和视频相机，奈奎斯特率可能非常高，导致我们最终得到过多的样本，必须进行压缩才能存储或传输。在其他应用中，包括成像系统（医学扫描仪、雷达）和高速模数转换器，将采样率或密度提高到超越当前技术水平是非常昂贵的。

在本讲座中，我们将学习一种利用压缩感知 [1, 2] 来解决这些问题的新技术。我们将用一种更通用的线性测量方案结合优化方法来取代传统的采样和重构操作，以便以显著低于奈奎斯特率的速率获取某些类型的信号。

2 相关性 (Relevance)

这里提出的思想可以用来阐明数据采集、线性代数、基展开、逆问题、压缩、降维和优化之间的联系，适用于从本科或研究生数字信号处理到统计学和应用数学的各种课程。

3 先决条件 (Prerequisites)

理解和讲授这些材料所需的先决条件是线性代数、基础优化和基础概率论。

4 问题陈述 (Problem Statement)

奈奎斯特率采样通过利用信号的带限性来完全描述信号。我们的目标是通过利用信号的可压缩性来减少完全描述信号所需的测量次数。特殊之处在于，我们的测量不是点采样，而是信号的更一般的线性泛函。

考虑一个实值、有限长度、一维的离散时间信号 $x$ ，我们将其视为 $R^{N}$ 中的一个 $N \times 1$ 列向量，其元素为 $x [n]$ ， $n = 1, 2, \dots, N$ 。对于图像或更高维的数据，我们通过将其向量化为一个长的一维向量来处理。

$R^{N}$ 中的任何信号都可以用一组 $N \times 1$ 的向量基 ${ψ_{i}}_{i = 1}^{N}$ 来表示。为简单起见，假设该基是标准正交基。将这些向量 ${ψ_{i}}$ 作为列堆叠起来，形成 $N \times N$ 的基矩阵 $Ψ : = [ψ_{1} | ψ_{2} | \cdot . . . | ψ_{N}]$ ，我们可以将任何信号 $x$ 表示为

x = \sum_{i = 1}^{N} s_{i} ψ_{i} 或 x = Ψ s (1)

其中 s 是 $N \times 1$ 的权重系数 $s_{i} = ⟨ x, ψ_{i} ⟩ = ψ_{i}^{T} x$ 的列向量， $\cdot^{T}$ 表示（厄米）转置操作。显然， $x$ 和 s 是同一信号的等价表示， $x$ 在时域，s 在 $Ψ$ 域。

我们将关注具有稀疏表示的信号，其中 $x$ 仅是 $K$ 个基向量的线性组合，且 $K ≪ N$ 。也就是说，(1) 中只有 $K$ 个 $s_{i}$ 是非零的，而 $(N - K)$ 个是零。稀疏性的动机在于，许多自然和人造信号都是可压缩的，即存在一个基 $Ψ$ ，使得表示 (1) 只有少数几个大系数和许多小系数。可压缩信号可以通过 $K$ -稀疏表示很好地近似；这是变换编码 [3] 的基础。例如，自然图像在离散余弦变换 (DCT) 和小波基 [3] 中往往是可压缩的，JPEG 和 JPEG-2000 压缩标准就是基于这些变换。音频信号和许多通信信号在局部傅里叶基中是可压缩的。

变换编码在像数码相机这样的数据采集系统中扮演着核心角色，这些系统中样本数量很高但信号是可压缩的。在这个框架中，我们采集完整的 $N$ 个样本信号 $x$ ；通过 $s = Ψ^{T} x$ 计算完整的变换系数集 ${s_{i}}$ ；找到 $K$ 个最大的系数并丢弃 $(N - K)$ 个最小的系数；然后编码这 $K$ 个最大系数的值和位置。（实践中，我们还会将值和位置转换为数字比特。）

不幸的是，这种“先采样后压缩”的框架存在三个固有的低效之处：首先，即使最终期望的 $K$ 很小，我们也必须从可能非常大的样本数 $N$ 开始。其次，编码器必须计算所有 $N$ 个变换系数 ${s_{i}}$ ，即使它将丢弃除了 $K$ 个之外的所有系数。第三，编码器面临着编码大系数位置的开销。

作为替代方案，我们将研究一种更通用的数据采集方法，该方法直接将信号压缩成一个表示，而无需经过采集 $N$ 个样本的中间阶段。考虑更一般的线性测量过程，该过程计算 $x$ 与一组向量 ${ϕ_{j}}_{j = 1}^{M}$ 之间的 $M < N$ 个内积，如 $y_{j} = ⟨ x, ϕ_{j} ⟩$ 。将测量值 $y_{j}$ 堆叠成 $M \times 1$ 的向量 y，并将测量向量 $ϕ_{j}^{T}$ 作为行堆叠成 $M \times N$ 的矩阵 $Φ$ ，代入 (1)，我们可以写出

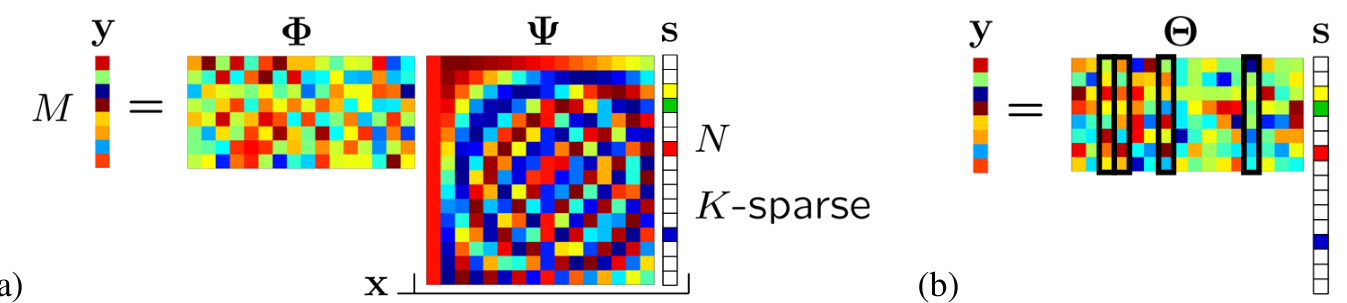图 1：(a) 压缩感知测量过程，使用（随机高斯）测量矩阵 $Φ$ 和离散余弦变换 (DCT) 矩阵 $Ψ$ 。系数向量 s 是稀疏的， $K = 4$ 。(b) 用矩阵乘积 $Θ = Φ Ψ$ 表示的测量过程，突出显示了对应于非零 $s_{i}$ 的四列。测量向量 y 是这四列的线性组合。

y = Φ x = Φ Ψ s = Θ s (2)

其中 $Θ Θ : = Φ Ψ$ 是一个 $M \times N$ 矩阵。参见图 1(a) 对 (2) 的图形描绘。注意测量过程是非自适应的；也就是说， $Φ$ 不以任何方式依赖于信号 $x$ 。

我们接下来的目标是设计一个测量矩阵 $Φ$ 和一个针对 $K$ -稀疏及可压缩信号的重构算法，该算法只需要 $M \approx K$ 或稍多的测量值，即大约与传统变换编码器编码的系数数量一样多的测量值。我们的方法基于最近在 [1, 2] 中介绍的压缩感知理论。

5 解决方案 (Solution)

解决方案包括两个步骤。第一步，我们设计一个稳定的测量矩阵 $Φ$ ，确保任何 $K$ -稀疏或可压缩信号中的显著信息不会因为从 $x \in R^{N}$ 到 $y \in R^{M}$ 的降维而受损。第二步，我们开发一个重构算法，从测量值 $y$ 中恢复 $x$ 。最初，我们专注于精确的 $K$ -稀疏信号。

5.1 稳定的测量矩阵 (Stable measurement matrix)

首先，我们设计数据采集系统的测量端，其核心是矩阵 $Φ$ 。我们的目标是进行 $M$ 次测量（得到向量 y），从中我们可以稳定地重构长度为 $N$ 的信号 $x$ ，或者等价地，重构其在基 $Ψ$ 中的稀疏系数向量 s。显然，如果测量过程损害了 $x$ 中的信息，重构将是不可能的。不幸的是，一般情况下确实如此：由于测量过程是线性的，并且由矩阵 $Φ$ 和 $Ψ$ 定义，根据 (2) 从 $y$ 求解 s 只是一个线性代数问题，而当 $M < N$ 时，方程数量少于未知数数量，使得解在一般情况下是不适定的 (ill-posed)。

然而，s 的 $K$ -稀疏性为我们提供了帮助。在这种情况下，测量向量 y 仅仅是 $Θ$ 中对应于 $s_{i} \neq 0$ 的 $K$ 列的线性组合（见图 1(b)）。因此，如果我们事先知道 s 中哪 $K$ 个元素是非零的，那么我们可以构建一个 $M \times K$ 的线性方程组来求解这些非零元素，此时方程的数量 $M$ 等于或超过未知数的数量 $K$ 。确保这个 $M \times K$ 系统是良态的 (well-conditioned) —— 从而具有稳定的逆 —— 的一个充分必要条件是，对于任何与 s 共享相同 $K$ 个非零项的向量 $v$ ，我们有

1 - ϵ \leq \frac{‖ Θ v ‖_{2}}{‖ v ‖_{2}} \leq 1 + ϵ (3)

对于某个 $ϵ > 0$ 。换句话说，矩阵 $Θ$ 必须保持这些特定的 $K$ -稀疏向量的长度。

当然，在实践中我们并不知道 s 中 $K$ 个非零项的位置。有趣的是，可以证明，对于 $K$ -稀疏和可压缩信号，一个稳定的逆的充分条件是 $Θ$ 对任意 $3 K$ -稀疏向量 $v$ 满足 (3)。这就是所谓的约束等距性 (Restricted Isometry Property, RIP) [1]。

另一种确保稳定性的方法是确保测量矩阵 $Φ$ 与稀疏化基 $Ψ$ 是不相干的 (incoherent)，即向量 ${ϕ_{j}}$ 不能稀疏地表示向量 ${ψ_{i}}$ ，反之亦然 [1, 2, 4]。经典的例子是 delta 脉冲和傅里叶正弦波分别扮演 ${ϕ_{j}}$ 和 ${ψ_{i}}$ 的角色；傅里叶不确定性原理直接产生了不相干性。

那么，给定一个稀疏化基 $Ψ$ ，我们如何构造一个测量矩阵 $Φ$ ，使得 $Θ = Φ Ψ$ 具有 RIP？不幸的是，仅仅验证一个给定的 $Θ$ 是否具有 RIP 在组合上是复杂的；我们必须对长度为 $N$ 的向量 $v$ 中 $(\binom{N}{K})$ 种可能的 $K$ 个非零项组合中的每一种验证 (3)。

在压缩感知中，我们通过选择 $Φ$ 为一个随机矩阵来回避这个问题。例如，我们将矩阵元素 $ϕ_{j, i}$ 作为独立同分布 (iid) 的随机变量从零均值、方差为 $1 / N$ 的高斯密度（白噪声）中抽取 [1, 2, 5]。然后，测量值 $y$ 仅仅是 $x$ 元素 $M$ 个不同的随机加权线性组合（回想图 1(a) 并注意 $Φ$ 的随机结构）。

高斯矩阵 $Φ$ 有两个有趣且有用的性质。首先， $Φ$ 与 delta 脉冲基 $Ψ = I$ 以高概率是不相干的，因为需要整整 $N$ 个脉冲才能表示 $Φ$ 的每一行。更严格地说，使用测度集中理论，可以证明一个 $M \times N$ 的 iid 高斯矩阵 $Θ = Φ I = Φ$ 在 $M \geq c K \log (N / K)$ （其中 $c$ 是一个小常数）的条件下，以高概率具有 RIP [1, 2, 5]。因此，我们可以期望以高概率从仅仅 $M \geq c K \log (N / K) ≪ N$ 个随机高斯测量中恢复长度为 $N$ 的 $K$ -稀疏和可压缩信号。其次，由于生成 $Φ$ 的 iid 高斯分布的性质，无论选择何种（标准正交）稀疏化基矩阵 $Ψ$ ，矩阵 $Θ = Φ Ψ$ 也是 iid 高斯的。因此，随机高斯测量 $Φ$ 是通用的，因为对于任何可能的 $Ψ$ ， $Θ = Φ Ψ$ 都以高概率具有 RIP。

除其他许多矩阵外，具有随机 $\pm 1$ 项的拉德马赫 (Rademacher) 矩阵也可以被证明具有 RIP 和通用性 [5]。

5.2 信号重构算法 (Signal reconstruction algorithms)

RIP 提供了理论保证，即一个 $K$ -稀疏或可压缩信号可以被 $y$ 中的 $M$ 个测量完全描述，但它没有告诉我们如何恢复它。信号重构步骤必须利用测量值 $y$ 、随机测量矩阵 $Φ$ （或生成它的随机种子）和稀疏化基 $Ψ$ 来重新生成长度为 $N$ 的信号 $x$ ，或者等价地，其稀疏系数向量 s。我们再次首先关注 $K$ -稀疏信号。

由于在 (2) 中 $M < N$ ，存在无限多个 $s^{'}$ 满足 $Θ Θ s^{'} = y$ ；它们都位于 $R^{N}$ 中维度为 $(N - M)$ 的超平面 $H : = N (Θ) + s$ 上，该超平面对应于 $Θ$ 的零空间 $N (Θ)$ 平移到真实的稀疏解 s。这是因为如果 $Θ Θ s = y$ ，那么对于零空间中的任何向量 $r$ ，都有 $Θ Θ (s + r) = y$ 。因此，我们的目标是在这个平移的零空间中找到信号的稀疏系数向量 s。

定义向量 s 的 $ℓ_{p}$ 范数为 $\begin{matrix} (‖ s ‖_{p})^{p} = \sum_{i = 1}^{N} | s_{i} |^{p} \end{matrix}$ 。当 $p = 0$ 时，我们得到 $ℓ_{0}$ “范数”，它计算 s 中非零项的数量；因此一个 $K$ -稀疏向量的 $ℓ_{0}$ 范数为 $K$ 。

最小 $ℓ_{2}$ 范数重构：解决这类逆问题的经典方法是最小二乘法；也就是说，我们选择在平移零空间 $H$ 中具有最小 $ℓ_{2}$ 范数（能量）的向量：

\hat{s} = a r g m i n ‖ s^{'} ‖_{2} 使 得 Θ s^{'} = y . (4)

甚至有一个方便的闭式解 $\hat{s} = Θ^{T} (Θ Θ^{T})^{- 1} y$ 。但不幸的是，当我们寻求的向量 s 是 $K$ -稀疏时， $ℓ_{2}$ 最小化几乎永远找不到它。我们得到的反而是一个非稀疏的 $\hat{s}$ ，并带有大量的振铃（更多内容见下文第 6.1 节）。

最小 $ℓ_{0}$ 范数重构：由于 (4) 中的 $ℓ_{2}$ 范数不反映信号稀疏性，一个合乎逻辑的替代方案是搜索平移零空间 $H$ 中最稀疏的向量：

\hat{s} = argmin ‖ s^{'} ‖_{0} 使 得 Θ s^{'} = y . (5)

可以证明，仅用 $M = K + 1$ 个 iid 高斯测量，这个优化就能以高概率精确恢复一个 $K$ -稀疏信号 [6]。但不幸的是，求解 (5) 既是数值不稳定的，也是一个 NP 完全问题，需要对 s 中非零项位置的所有 $(\binom{N}{K})$ 种可能组合进行穷举搜索。

最小 $ℓ_{1}$ 范数重构：压缩感知的惊奇之处在于，从 $M \geq c K \log (N / K)$ 个 iid 高斯测量中，我们可以通过 $ℓ_{1}$ 优化 [1, 2] 以高概率精确地重构 $K$ -稀疏向量，并稳定地逼近可压缩向量：

\hat{s} = a r g m i n ‖ s^{'} ‖_{1} 使 得 Θ s^{'} = y . (6)

这是一个凸优化问题，可以方便地简化为一个称为基追踪 (Basis Pursuit) [1, 2] 的线性规划问题，其计算复杂度约为 $O (N^{3})$ 。

总结来说，一个压缩感知数据采集系统包括基于 $Φ$ 的随机测量，然后通过线性规划重构得到 x。

6 讨论 (Discussion)

6.1 几何解释 (Geometrical interpretation)

$R^{N}$ 中压缩感知问题的几何结构有助于我们理解为什么 $ℓ_{1}$ 重构成功而 $ℓ_{2}$ 重构失败。首先，注意 $R^{N}$ 中所有 $K$ -稀疏向量 s 的集合是一个高度非线性的空间，由所有与坐标轴对齐的 $K$ 维超平面组成（见图 2(a)）。因此，稀疏向量位于 $R^{N}$ 中靠近坐标轴的地方。

为了形象化 $ℓ_{2}$ 重构失败的原因，注意平移零空间 $H = N (Θ) + s$ 的维度是 $(N - M)$ ，并且由于矩阵 $Θ$ 的随机性，它以一个随机的角度定向。参见图 2(b)，但要注意在实践中 $N, M, K ≫ 3$ ，所以你需要将你的直觉推广到高维空间。来自 (4) 的 $ℓ_{2}$ 最小化解 $\hat{s}$ 是 $H$ 上离原点最近的点。我们可以通过膨胀一个超球面（ $ℓ_{2}$ 球）直到它接触 $H$ 来找到这个点。由于 $H$ 的随机方向，最近点 $\hat{s}$ 将以高概率远离坐标轴，因此既不是稀疏的，也不接近正确的答案 s。

与 $ℓ_{2}$ 球形成鲜明对比的是，图 2© 中的 $ℓ_{1}$ 球是“尖的”，其尖点沿着坐标轴对齐（并且随着环境维度 $N$ 的增长变得更尖）。因此，当我们膨胀 $ℓ_{1}$ 球时，它将首先在靠近坐标轴的点接触平移零空间 $H$ ，而这正是稀疏向量 s 所在的位置。

6.2 模拟信号 (Analog signals)

虽然我们主要关注离散时间信号 $x$ ，压缩感知也适用于模拟信号 $x (t)$ ，这些信号可以使用来自某个连续基或字典 ${ψ_{i} (t)}_{i = 1}^{N}$ 中仅 $K$ 个（共 $N$ 个）元素进行稀疏表示。虽然每个 $ψ_{i} (t)$ 可能具有很宽的带宽（因此具有很高的奈奎斯特率），但信号 $x (t)$ 只有 $K$ 个自由度，我们可以应用上述理论以低于奈奎斯特率的速率对其进行测量。一个实用的模拟压缩感知系统的例子——所谓的“模拟到信息”转换器——在 [7] 中给出；这与 [8] 有着有趣的联系。

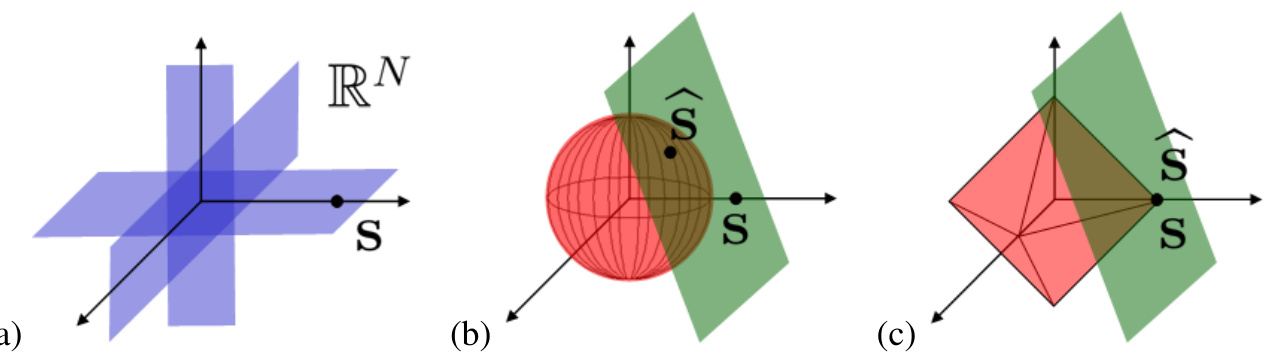图 2：(a) 稀疏向量 s 位于 $R^{N}$ 中与坐标轴对齐的 $K$ 维超平面上，因此靠近坐标轴。(b) 通过 $ℓ_{2}$ 最小化进行的压缩感知恢复没有找到平移零空间（绿色超平面）上正确的稀疏解 s，而是找到了非稀疏向量 $\hat{s}$ 。© 通过 $ℓ_{1}$ 最小化进行的恢复，在有足够测量值的情况下，确实找到了正确的稀疏解 s。

7 实例应用 (Practical Example)

考虑图 3(a) 中的“单像素”压缩数字相机，它直接获取 $M$ 个随机线性测量值，而无需首先收集 $N$ 个像素值 [9]。对应于所需图像 x 的入射光场并未聚焦到 CCD 或 CMOS 采样阵列上，而是从一个由 $N$ 个微小反射镜组成的数字微镜器件 (Digital Micromirror Device, DMD) 反射。（DMD 存在于许多计算机投影仪和投影电视内部。）然后反射光被第二个透镜收集并聚焦到单个光电二极管（单像素）上。每个反射镜可以独立地朝向光电二极管（对应于 1）或远离光电二极管（对应于 0）。每个测量值 $y_{j}$ 的获取过程如下：随机数生成器 (RNG) 以伪随机的 0/1 模式设置反射镜方向，以创建测量向量 $ϕ_{j}$ 。光电二极管处的电压随后等于 $y_{j}$ ，即 $ϕ_{j}$ 与所需图像 $x$ 的内积。该过程重复 $M$ 次以获取 $y$ 中的所有条目。

图 3(b) 和 © 展示了一个目标物体和由单像素相机原型 [9] 拍摄的图像 $\hat{x}$ ，其使用的随机测量次数比重构的像素数少了约 $60 %$ 。这里的重构是通过全变分优化 [1] 进行的，这与小波域中的 $ℓ_{1}$ 重构密切相关。

单像素压缩感知方法的一个主要优点是，这种相机可以适用于在难以或昂贵地制造大型传感器阵列的波长下成像。它还可以随时间采集数据以实现视频重构 [9]。

8 结论 (Conclusions)

在本讲座中，我们了解到采样并不是获取信号的唯一途径。当感兴趣的信号是可压缩或稀疏的时，采用随机测量和优化方法，仅获取我们需要的测量值，可能更高效、更简洁。我们还了解到，对于重构问题，我们熟悉的老朋友最小二乘法失效了，我们需要寻求其他形式的凸优化方法，如线性规划（另见 [4, 10]）。压缩感知仍然是一个新兴领域，许多有趣的研究问题仍有待解决。关于当前研究方向的相当详尽的参考文献列表可在 dsp.rice.edu/cs 获取。

图 3：(a) 单像素压缩感知相机。(b) 传统数码相机拍摄的足球图像。© 从 (a) 中相机获取的 $M = 1600$ 个随机测量值恢复的同一足球的 $64 \times 64$ 黑白图像 x（ $N = 4096$ 像素）。(b) 和 © 中的图像并非刻意对齐。

References

[1] E. Cand`es, J. Romberg, and T. Tao, “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inform. Theory, vol. 52, no. 2, pp. 489–509, Feb. 2006.
[2] D. Donoho, “Compressed sensing,” IEEE Trans. Inform. Theory, vol. 52, no. 4, pp. 1289– 1306, April 2006.
[3] S. Mallat, A Wavelet Tour of Signal Processing. Academic Press, 1999.
[4] J. Tropp and A. C. Gilbert, “Signal recovery from partial information via orthogonal matching pursuit,” April 2005, www-personal.umich.edu/∼jtropp/papers/TG05-Signal-Recovery.pdf.
[5] R. G. Baraniuk, M. Davenport, R. DeVore, and M. B. Wakin, “The Johnson-Lindenstrauss lemma meets compressed sensing,” 2006, dsp.rice.edu/cs/jlcs-v03.pdf.
[6] D. Baron, M. B. Wakin, M. Duarte, S. Sarvotham, and R. G. Baraniuk, “Distributed compressed sensing,” 2005, dsp.rice.edu/cs/DCS112005.pdf.
[7] S. Kirolos, J. Laska, M. Wakin, M. Duarte, D. Baron, T. Ragheb, Y. Massoud, and R. G. Baraniuk, “Analog-to-information conversion via random demodulation,” in IEEE Dallas Circuits and Systems Workshop, Oct. 2006.
[8] M. Vetterli, P. Marziliano, and T. Blu, “Sampling signals with finite rate of innovation,” IEEE Trans. Signal Processing, vol. 50, no. 6, pp. 1417–1428, June 2002.
[9] D. Takhar, V. Bansal, M. Wakin, M. Duarte, D. Baron, J. Laska, K. F. Kelly, and R. G. Baraniuk, “A compressed sensing camera: New theory and an implementation using digital micromirrors,” in Proc. Comput. Imaging IV at SPIE Electronic Imaging, San Jose, Jan. 2006.
[10] J. Haupt and R. Nowak, “Signal reconstruction from noisy random projections,” IEEE Trans. Inform. Theory, vol. 52, no. 9, pp. 4036–4048, Sept. 2006.

致谢 (Acknowledgements): 这项工作得到了 NSF、DARPA、ONR、AFOSR 和德州仪器领导力大学计划 (Texas Instruments Leadership University Program) 的资助。感谢莱斯大学 DSP 小组和 Ron DeVore 带来的许多富有启发性的讨论。感谢 Justin Romberg 在图 3 重构方面的帮助。

作者 (Author): Richard G. Baraniuk 是莱斯大学电子与计算机工程系的 Victor E. Cameron 教授。他的研究兴趣包括多尺度分析、逆问题、分布式信号处理和传感器网络。他的研究获得了美国国家科学基金会 (US National Science Foundation) 和海军研究办公室 (Office of Naval Research) 的国家青年研究者奖 (National Young Investigator awards)，以及莱斯大学和伊利诺伊大学的成就奖。他的教学获得了 Eta Kappa Nu 颁发的 C. Holmes MacDonald 国家杰出教学奖 (National Outstanding Teaching Award)，并三次获得莱斯大学的 George R. Brown 卓越教学奖 (Award for Superior Teaching)。他于 2001 年当选为 IEEE Fellow。